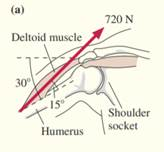
The deltoid—the rounded muscle across the top of your upper arm—allows you to lift your arm away from your side. It does so by pulling on an attachment point on the humerus, the upper arm bone, at an angle of 15° with respect to the humerus. If you hold your arm at an angle 30° below horizontal, the deltoid must pull with a force of 720 N to support the weight of your arm, as shown in FIGURE 3.21a. (You’ll learn in Chapter 5 that force is a vector
The correct answer and explanation is:
To solve the problem of determining the force that the deltoid muscle applies, we need to analyze the forces involved in supporting the weight of the arm while it is at an angle of 30° below horizontal.
Step 1: Understanding the forces
The deltoid muscle generates a force to counteract the force of gravity acting on the arm. The force of gravity is acting vertically downward on the arm’s mass, which can be represented as the weight of the arm. The deltoid muscle, however, is pulling at an angle of 15° relative to the horizontal, so the force it generates has both a vertical and horizontal component.
Step 2: Resolving the force of the deltoid muscle
When a force is applied at an angle, it can be broken into two components: the vertical component (which counters the weight of the arm) and the horizontal component (which helps to stabilize the arm). The force the deltoid muscle applies, FdeltoidF_{\text{deltoid}}, can be decomposed into two components:
- Vertical component: Fdeltoidsin(15∘)F_{\text{deltoid}} \sin(15^\circ)
- Horizontal component: Fdeltoidcos(15∘)F_{\text{deltoid}} \cos(15^\circ)
Step 3: Balancing forces
Since the deltoid muscle needs to counteract the weight of the arm, the vertical component of the muscle’s force must equal the weight of the arm. Given that the force needed to support the arm is 720 N at a 30° angle below the horizontal, this force supports both the weight and stabilizes the arm at that angle.
Therefore, the vertical component of the deltoid force must satisfy the equation: Fdeltoidsin(15∘)=720 NF_{\text{deltoid}} \sin(15^\circ) = 720 \, \text{N}
Solving for the deltoid force, FdeltoidF_{\text{deltoid}}: Fdeltoid=720 Nsin(15∘)≈720 N0.2588≈2785.7 NF_{\text{deltoid}} = \frac{720 \, \text{N}}{\sin(15^\circ)} \approx \frac{720 \, \text{N}}{0.2588} \approx 2785.7 \, \text{N}
Thus, the deltoid must apply a force of approximately 2786 N to support the weight of the arm while it is at the specified angle.
Explanation:
The reason the deltoid applies such a large force compared to the weight of the arm is due to the mechanical advantage provided by the angle at which the muscle pulls. Since the muscle’s force is at an angle to the humerus, only a component of the muscle’s force is effectively supporting the weight. This means that a much greater force is needed to balance the weight, which explains the large value of 2786 N. The geometry of muscle forces is a key factor in understanding how much force the body must generate to support various movements.