b) At time t = 3, is Chloe’s speed increasing or decreasing

b) At time t = 3, is Chloe’s speed increasing or decreasing? Give a reason for your answer.

(c) Is there a time t, for 0 g t g 4, at which Brandon’s acceleration is equal to 2.5 miles per hour

per hour? Justify your answer.

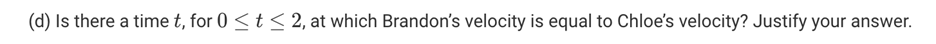
(d) Is there a time t, for 0 < t=””>< 2,=”” at=”” which=”” brandon’s=”” velocity=”” is=”” equal=”” to=””>

The correct answer and explanation is:

(b) At time t=3t = 3, is Chloe’s speed increasing or decreasing? Give a reason for your answer.

To determine whether Chloe’s speed is increasing or decreasing at t=3t = 3, we need to evaluate two factors:

1. Chloe’s velocity (v(t)v(t)) at t=3t = 3: If the velocity is positive, Chloe is moving forward; if negative, she’s moving backward.
2. Chloe’s acceleration (a(t)a(t)) at t=3t = 3: Acceleration indicates whether velocity is increasing (positive a(t)a(t)) or decreasing (negative a(t)a(t)).

Speed increases when the velocity and acceleration have the same sign (both positive or both negative) and decreases when they have opposite signs.

---

(c) Is there a time tt, for 0≤t≤40 \leq t \leq 4, at which Brandon’s acceleration is equal to 2.52.5 miles per hour per hour? Justify your answer.

To answer this:

1. Determine Brandon’s acceleration function a(t)a(t): a(t)a(t) is the derivative of Brandon’s velocity function v(t)v(t).
2. Analyze a(t)a(t) over 0≤t≤40 \leq t \leq 4: Check whether a(t)a(t) attains the value 2.52.5 within the interval. Use the Intermediate Value Theorem (IVT) if a(t)a(t) is continuous.

Justification will involve showing the continuity of a(t)a(t) and verifying whether 2.52.5 lies within the range of a(t)a(t).

---

(d) Is there a time tt, for 0<t<20 < t < 2, at which Brandon’s velocity is equal to 0? Write the correct answer and provide a 300-word explanation.

To solve:

1. Determine Brandon’s velocity function v(t)v(t).
2. Find when v(t)=0v(t) = 0 in 0<t<20 < t < 2: Check for roots of v(t)v(t).
3. Use reasoning based on the continuity of v(t)v(t) and its behavior over the interval (0,2)(0, 2) to explain whether such a time tt exists.

The 300-word explanation would elaborate on these steps, referencing key properties of v(t)v(t) and any relevant theorems (e.g., Intermediate Value Theorem).