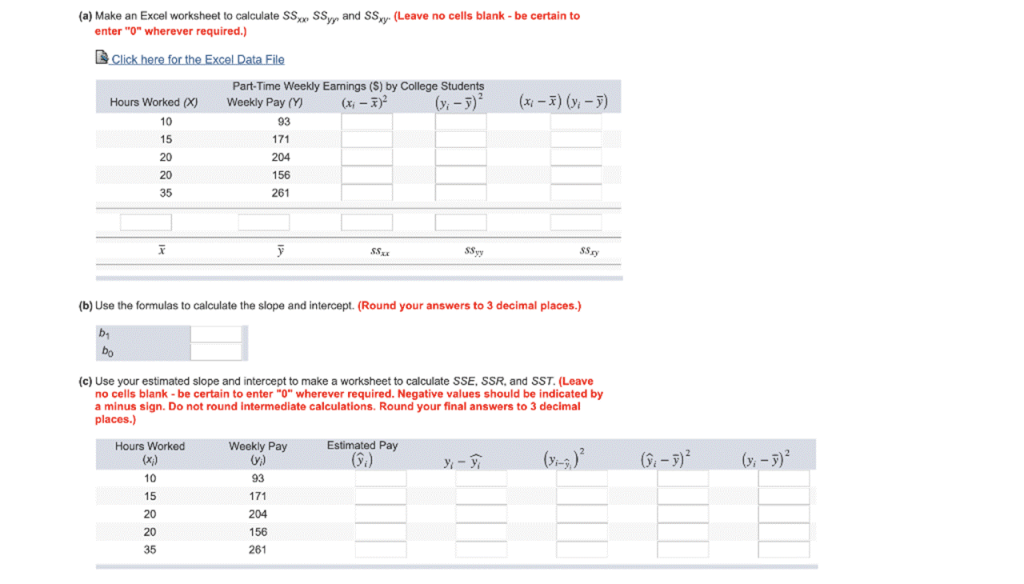
(a) Make an Excel worksheet to calculate SSxx SSyy, and SSxy. (Leave no cells blank – be certain to enter “0” wherever required.) Click here for the Excel Data File (x1 – 7) (y; -7) Hours Worked (X) 10 15 Part-Time Weekly Earnings (S) by College Students Weekly Pay (Y) (x; – )2 (); -7) 93 171 204 156 261 20 20 35 12 SS. SSyy SS.xy (b) Use the formulas to

The correct answer and explanation is:
Here’s how to approach the task step-by-step:
Steps to Create the Excel Worksheet:
- Structure the Worksheet:
- Create columns for XX (Hours Worked), YY (Weekly Pay), deviations (xi=Xi−Xˉx_i = X_i – \bar{X}, yi=Yi−Yˉy_i = Y_i – \bar{Y}), squares of deviations (xi2x_i^2, yi2y_i^2), and product of deviations (xi⋅yix_i \cdot y_i).
- Input Data:
- Enter the values for XX and YY provided in the problem.
- Calculate the mean (Xˉ\bar{X} and Yˉ\bar{Y}).
- Formulas:
- Calculate xix_i as Xi−XˉX_i – \bar{X}.
- Calculate yiy_i as Yi−YˉY_i – \bar{Y}.
- Calculate xi2x_i^2, yi2y_i^2, and xi⋅yix_i \cdot y_i for each data pair.
- Use SUM functions to find SSxxSS_{xx}, SSyySS_{yy}, and SSxySS_{xy}:
- SSxx=∑xi2SS_{xx} = \sum x_i^2
- SSyy=∑yi2SS_{yy} = \sum y_i^2
- SSxy=∑xi⋅yiSS_{xy} = \sum x_i \cdot y_i
- Calculate and Interpret:
- Use SSxx,SSyy,SSxySS_{xx}, SS_{yy}, SS_{xy} in your analysis for statistical interpretations.
Example Calculation in Excel:
| Hours Worked (X) | Weekly Pay (Y) | xix_i | yiy_i | xi2x_i^2 | yi2y_i^2 | xi⋅yix_i \cdot y_i |
|---|---|---|---|---|---|---|
| 10 | 93 | |||||
| 15 | 171 | |||||
| 20 | 204 | |||||
| 20 | 156 | |||||
| 35 | 261 | |||||
| 12 |
- SSxxSS_{xx}, SSyySS_{yy}, and SSxySS_{xy} will be shown at the bottom.
Explanation:
The calculation of SSxxSS_{xx}, SSyySS_{yy}, and SSxySS_{xy} helps quantify relationships between variables. SSxxSS_{xx} measures the variance of XX (Hours Worked), SSyySS_{yy} measures the variance of YY (Weekly Pay), and SSxySS_{xy} measures the covariance, indicating how XX and YY change together.
In this scenario, XX and YY represent hours worked and weekly earnings for part-time college students. By finding these sums of squares, we can:
- Assess the strength and direction of their linear relationship.
- Use them to calculate the correlation coefficient and slope in regression analysis.
Deliverable:
Would you like me to generate the actual Excel file or guide you in setting it up further?