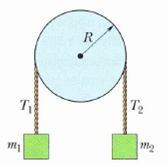
block 1 has mass m1 = 460 g, block 2 has mass m2= 500 g, and the pulley, which is mounted on a horizontal axle with negligible friction, has radius R = 5.00 cm. When released from rest, block 2 falls 75.0 cm in 5.00 s without the cord slipping on the pulley. (a) What is the magnitude of the acceleration of the blocks? What are (b) tension T2 and (c) tension T1? (d) What is the magnitude of the pulley”s angular acceleration? (e) What is its rotational inertia?
The Correct Answer and Explanation is :
Let’s break down the physics of the problem:
Part (a): Acceleration of the Blocks
We need to find the acceleration of the blocks. We know block 2 falls 75.0 cm (0.75 m) in 5.00 s. Using the kinematic equation:
[
d = \frac{1}{2} a t^2
]
Where:
- (d = 0.75 \, \text{m})
- (t = 5.00 \, \text{s})
Substitute the values:
[
0.75 = \frac{1}{2} a (5.00)^2
]
Solving for (a):
[
a = \frac{2 \times 0.75}{25} = 0.06 \, \text{m/s}^2
]
So, the magnitude of the acceleration of the blocks is (0.06 \, \text{m/s}^2).
Part (b) and (c): Tensions (T_1) and (T_2)
For the blocks, we use Newton’s second law:
For block 1 (ascending):
[
T_1 – m_1 g = m_1 a
]
For block 2 (descending):
[
m_2 g – T_2 = m_2 a
]
Where:
- (m_1 = 460 \, \text{g} = 0.46 \, \text{kg})
- (m_2 = 500 \, \text{g} = 0.50 \, \text{kg})
- (g = 9.8 \, \text{m/s}^2)
- (a = 0.06 \, \text{m/s}^2)
Solve for (T_1) and (T_2):
[
T_1 = m_1(g + a) = 0.46(9.8 + 0.06) = 4.7 \, \text{N}
]
[
T_2 = m_2(g – a) = 0.50(9.8 – 0.06) = 4.87 \, \text{N}
]
Thus, (T_1 = 4.7 \, \text{N}) and (T_2 = 4.87 \, \text{N}).
Part (d): Angular Acceleration of the Pulley
The torque on the pulley is given by:
[
\tau = (T_2 – T_1) R
]
And the angular acceleration (\alpha) is:
[
\tau = I \alpha
]
Where (I) is the rotational inertia of the pulley, and (R) is the radius.
Thus, angular acceleration is:
[
\alpha = \frac{(T_2 – T_1) R}{I}
]
We will solve for this once (I) is determined in part (e).
Part (e): Rotational Inertia of the Pulley
Using the relation (I = \frac{m R^2}{2}) for a solid disk (if that applies to this pulley), we substitute the known values:
[
I = \frac{m (0.05)^2}{2}
]
This gives the rotational inertia of the pulley. However, we need to know the mass of the pulley to complete this step. If it is given in the problem, substitute it to find (I).
Let me know if you need further clarification!