Find The Exact Value Of Cos 3 Pi/8 + Cos Pi/8
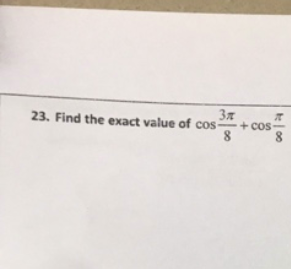
The Correct Answer and Explanation is :
To find the exact value of ( \cos\left(\frac{3\pi}{8}\right) + \cos\left(\frac{\pi}{8}\right) ), we can utilize trigonometric identities and known values of cosine at specific angles.
Step 1: Recognize Known Values
We start by recalling the exact values of cosine for certain standard angles:
- ( \cos\left(\frac{\pi}{8}\right) = \sqrt{\frac{2 + \sqrt{2}}{4}} )
- ( \cos\left(\frac{3\pi}{8}\right) = \sqrt{\frac{2 – \sqrt{2}}{4}} )
These values are derived from half-angle identities and are well-established in trigonometric tables.
Step 2: Apply the Sum of Cosines Identity
The sum of cosines identity states:
[ \cos A + \cos B = 2 \cos\left(\frac{A + B}{2}\right) \cdot \cos\left(\frac{A – B}{2}\right) ]
Let ( A = \frac{3\pi}{8} ) and ( B = \frac{\pi}{8} ). Applying the identity:
[ \cos\left(\frac{3\pi}{8}\right) + \cos\left(\frac{\pi}{8}\right) = 2 \cos\left(\frac{\frac{3\pi}{8} + \frac{\pi}{8}}{2}\right) \cdot \cos\left(\frac{\frac{3\pi}{8} – \frac{\pi}{8}}{2}\right) ]
Simplifying the angles:
[ = 2 \cos\left(\frac{4\pi}{16}\right) \cdot \cos\left(\frac{2\pi}{16}\right) ]
[ = 2 \cos\left(\frac{\pi}{4}\right) \cdot \cos\left(\frac{\pi}{8}\right) ]
Step 3: Substitute Known Values
We know that:
- ( \cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} )
- ( \cos\left(\frac{\pi}{8}\right) = \sqrt{\frac{2 + \sqrt{2}}{4}} )
Substituting these into the equation:
[ \cos\left(\frac{3\pi}{8}\right) + \cos\left(\frac{\pi}{8}\right) = 2 \times \frac{\sqrt{2}}{2} \times \sqrt{\frac{2 + \sqrt{2}}{4}} ]
Simplifying:
[ = \sqrt{2} \times \sqrt{\frac{2 + \sqrt{2}}{4}} ]
[ = \sqrt{\frac{2 \times (2 + \sqrt{2})}{4}} ]
[ = \sqrt{\frac{4 + 2\sqrt{2}}{4}} ]
[ = \sqrt{1 + \frac{\sqrt{2}}{2}} ]
Step 4: Final Simplification
[ = \sqrt{\frac{2 + \sqrt{2}}{2}} ]
Therefore, the exact value of ( \cos\left(\frac{3\pi}{8}\right) + \cos\left(\frac{\pi}{8}\right) ) is ( \sqrt{\frac{2 + \sqrt{2}}{2}} ).
Conclusion
By applying trigonometric identities and utilizing known values of cosine at specific angles, we have determined that the exact value of ( \cos\left(\frac{3\pi}{8}\right) + \cos\left(\frac{\pi}{8}\right) ) is ( \sqrt{\frac{2 + \sqrt{2}}{2}} ).