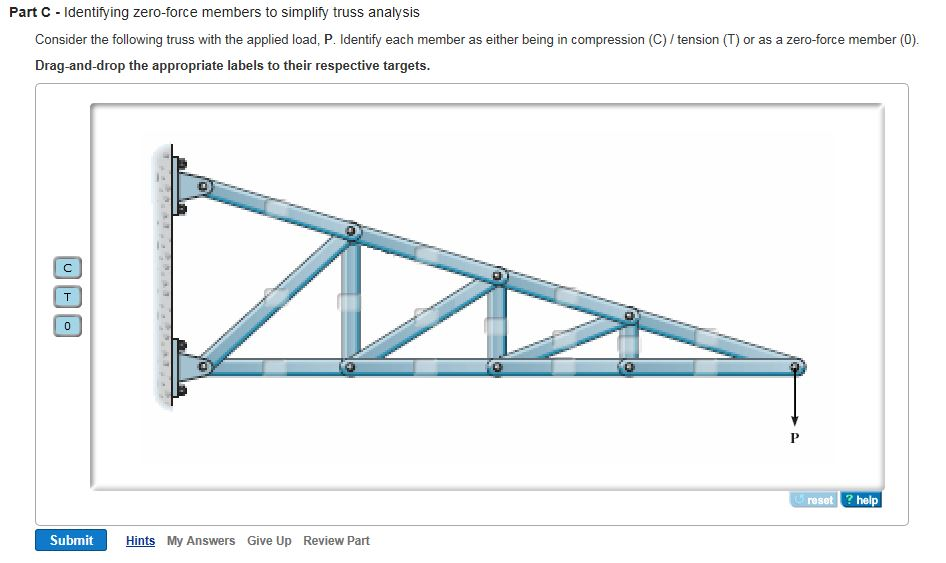
To be able to identify zero-force members in truss systems. Zero-force members in a truss usually can be determined by inspecting joints. Identify the unloaded joints in the truss. To start, choose an unloaded joint with the least amount of members connected to it. Then, draw a free-body diagram of the joint and determine whether zero-force members are present. After evaluating the joint, move on to another joint until all the joints have been evaluated. When determining whether zero-force members are present, there are two cases that need to be considered. One is when two members are connected at a right angle and there is no external load on the joint. For equilibrium to be maintained at the joint, each member must be a zero-force member. The other case is when two collinear members and one non-collinear member are connected at a joint with either no external loading or only loading in the same direction as the collinear members. In this case, the non-collinear member is a zero-force member (for static equilibrium to be maintained) because all forces (internal and external) are applied in one direction. You can identify these members by using the method of joints. Draw a free-body diagram of each joint and apply equilibrium equations ?Fx=0 and ?Fy=0 , where x and y refer to the coordinate system applied at each joint.
The Correct Answer and Explanation is :
To identify zero-force members in a truss system, we must analyze the structure using two primary cases and inspect the joints carefully. Here’s how to approach the problem using the provided diagram (though I can’t view the image directly, I’ll guide you through the general method):
Step-by-Step Process:
- Identify Unloaded Joints: Look for joints that have no external load applied. These joints are key to determining zero-force members. Unloaded joints are often located at the outer edges of the truss structure.
- Examine Joints with Two Members:
- Case 1: If a joint has only two members and no external load or support reaction, these two members must both be zero-force members. This is because for the joint to be in equilibrium, there is no need for forces in these two directions. Thus, both members at this joint do not carry any load.
- Examine Joints with Three Members (Two Collinear and One Non-Collinear):
- Case 2: If three members are connected at a joint, and two of them are collinear (aligned along the same line) while the third is non-collinear, and there is no external load or support at that joint, the non-collinear member must be a zero-force member. This is because the two collinear members will carry the load in a straight line, leaving the non-collinear member unnecessary for equilibrium.
- Apply Equilibrium Equations: Once you’ve identified potential zero-force members from these cases, apply the equilibrium conditions for each joint:
- ∑Fx=0\sum F_x = 0 (Sum of forces in the x-direction is zero)
- ∑Fy=0\sum F_y = 0 (Sum of forces in the y-direction is zero)
Example Explanation:
Consider a truss with a joint having only two members. Since there’s no external load at that joint, both members must carry zero load for equilibrium. Similarly, if you find a joint with two collinear members and one non-collinear member, and there’s no external load, the non-collinear member must be zero-force to maintain static equilibrium.
Summary:
By inspecting the truss joints and applying the principles of equilibrium, you can identify which members are zero-force members. The two cases (two members at a right angle or two collinear members with one non-collinear member) help you systematically reduce the number of unknown forces in the structure, simplifying the analysis of the truss.