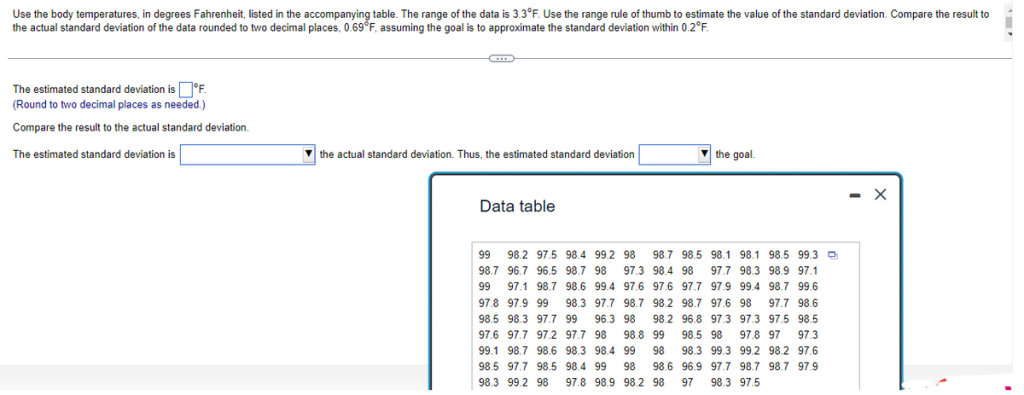
Use the body temperatures, in degrees Fahrenheit, listed in the accompanying table. The range of the data is 3.3°F. Use the range rule of thumb to estimate the value of the standard deviation. Compare the result to the actual standard deviation of the data rounded to two decimal places, 0.69°F, assuming the goal is to approximate the standard deviation within 0.2°F
The Correct Answer and Explanation is :
To estimate the standard deviation using the range rule of thumb, follow these steps:
Step 1: Recall the Range Rule of Thumb
The range rule of thumb estimates the standard deviation ((s)) as approximately:
[
s \approx \frac{\text{Range}}{4}
]
Step 2: Calculate the Estimated Standard Deviation
The given range of the data is (3.3^\circ\text{F}). Using the formula:
[
s \approx \frac{3.3}{4} = 0.825
]
Step 3: Compare to the Actual Standard Deviation
The actual standard deviation is given as (0.69^\circ\text{F}). Comparing the two values:
[
\text{Estimated Standard Deviation: } 0.825 \
\text{Actual Standard Deviation: } 0.69
]
Step 4: Assess the Accuracy
To determine whether the estimated standard deviation meets the goal, calculate the difference:
[
|0.825 – 0.69| = 0.135
]
The difference, (0.135), is less than the allowable tolerance of (0.2^\circ\text{F}). Thus, the estimated standard deviation is sufficiently close to the actual standard deviation.
Explanation
The range rule of thumb provides a quick and simple way to approximate the standard deviation, using only the range of the data. By dividing the range by 4, we get a rough estimate, assuming the data is roughly evenly distributed and follows a normal distribution. This method is particularly useful when a detailed calculation is unnecessary or when access to computational tools is limited.
In this case, the estimated standard deviation of (0.825^\circ\text{F}) is close to the actual value of (0.69^\circ\text{F}), differing by (0.135^\circ\text{F}), which is within the acceptable margin of (0.2^\circ\text{F}). Therefore, the range rule of thumb works well for this dataset, providing a reasonable approximation.
This result highlights the utility of the range rule of thumb as a quick estimation method, especially when analyzing data without advanced statistical software.