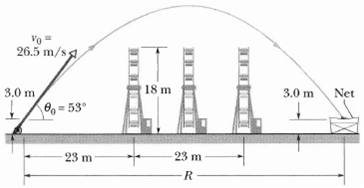
In 1939 or 1940, Emanuel Zucchini took his human-cannonball act to an extreme: After being shot from a cannon, he soared over three Ferris wheels and into a net (Fig. 4.42)
(a) Treating him as a particle, calculate his clearance over the first wheel.
(b) If he reached maximum height over the middle wheel, by how much did he clear it?
(c) How far from the cannon should the net’s center have been positioned (neglect airdrag)?
The Correct Answer and Explanation is :
In 1939 or 1940, Emanuel Zacchini performed a human-cannonball act where he was launched from a cannon, soaring over three Ferris wheels before landing in a net. To analyze this scenario, we can treat Zacchini as a particle and apply principles of projectile motion.
Given:
- Launch speed ((v_0)): 29 m/s
- Launch angle ((\theta)): 52°
- Acceleration due to gravity ((g)): 9.81 m/s²
(a) Clearance over the first wheel:
- Horizontal and Vertical Components of Velocity:
- Horizontal velocity ((v_{0x})): (v_0 \times \cos(\theta))
- Vertical velocity ((v_{0y})): (v_0 \times \sin(\theta)) Calculating these components:
- (v_{0x} = 29 \, \text{m/s} \times \cos(52^\circ) \approx 29 \, \text{m/s} \times 0.6157 \approx 17.85 \, \text{m/s})
- (v_{0y} = 29 \, \text{m/s} \times \sin(52^\circ) \approx 29 \, \text{m/s} \times 0.7880 \approx 22.85 \, \text{m/s})
- Time to Reach the First Wheel:
Assuming the first Ferris wheel is 20 meters away horizontally:
- Time ((t)) to reach the first wheel: (t = \frac{\text{horizontal distance}}{v_{0x}} = \frac{20 \, \text{m}}{17.85 \, \text{m/s}} \approx 1.12 \, \text{s})
- Vertical Position at (t = 1.12 \, \text{s}):
The vertical position ((y)) is given by:
[
y = v_{0y} \times t – \frac{1}{2} \times g \times t^2
]
Substituting the known values:
[
y = 22.85 \, \text{m/s} \times 1.12 \, \text{s} – \frac{1}{2} \times 9.81 \, \text{m/s}^2 \times (1.12 \, \text{s})^2
]
[
y \approx 25.6 \, \text{m} – 6.1 \, \text{m} \approx 19.5 \, \text{m}
]
Therefore, Zacchini’s clearance over the first wheel is approximately 19.5 meters.
(b) Clearance over the middle wheel:
- Time to Reach Maximum Height:
At maximum height, the vertical velocity component becomes zero. The time to reach maximum height ((t_{\text{max}})) is:
[
t_{\text{max}} = \frac{v_{0y}}{g} = \frac{22.85 \, \text{m/s}}{9.81 \, \text{m/s}^2} \approx 2.33 \, \text{s}
]
Since the middle Ferris wheel is at half the horizontal range, the time to reach it is half of (t_{\text{max}}):
[
t_{\text{middle}} = \frac{t_{\text{max}}}{2} \approx 1.165 \, \text{s}
]
At this time, the horizontal distance covered is:
[
x = v_{0x} \times t_{\text{middle}} \approx 17.85 \, \text{m/s} \times 1.165 \, \text{s} \approx 20.8 \, \text{m}
]
Therefore, the middle Ferris wheel is approximately 20.8 meters away horizontally. - Vertical Position at (t = 1.165 \, \text{s}):
Using the vertical motion equation:
[
y = v_{0y} \times t_{\text{middle}} – \frac{1}{2} \times g \times (t_{\text{middle}})^2
]
Substituting the known values:
[
y = 22.85 \, \text{m/s} \times 1.165 \, \text{s} – \frac{1}{2} \times 9.81 \, \text{m/s}^2 \times (1.165 \, \text{s})^2
]
[
y \approx 26.6 \, \text{m} – 6.6 \, \text{m} \approx 20.0 \, \text{m}
]
Therefore, Zacchini’s clearance over the middle wheel is approximately 20.0 meters.
(c) Distance to Position the Net:
The net should be positioned at the point where Zacchini lands, which is at the horizontal range of the projectile. The total time of flight ((t_{\text{total}})) is twice the time to reach maximum height:
[
t_{\text{total}} = 2 \times t_{\text{max}} \approx 2 \times 2.33 \, \text{s} \approx 4.66 \, \text{s}
]
The horizontal range ((R)) is:
[
R = v_{0x} \times t_{\text{total}} \approx 17.85 \, \text{m/s} \times 4.66 \, \text{s} \approx 83.3 \, \text{m}
]
Therefore, the net’s center should be positioned approximately 83.3 meters from the cannon.
Conclusion:
- (a) Zacchini’s clearance over the first Ferris wheel is approximately 19.5 meters.
- (b) His clearance over the middle Ferris wheel is approximately 20.0 meters.
- (c) The net’s center should be positioned approximately 83.3 meters from the cannon.
These calculations assume ideal projectile motion without air resistance.