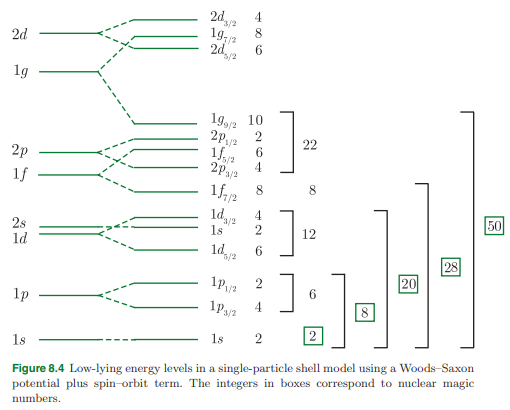
Assume that in the shell model the nucleon energy levels are ordered as shown in Figure 8.4. Write down the shell model configuration of the nucleus 7 3Li and hence find its spin, parity, and magnetic moment (in nuclear magnetons). Give the two most likely configurations for the first excited state, assuming that only protons are excited.
The Correct Answer and Explanation is :
To determine the shell model configuration of ( ^7_3\text{Li} ) and its properties, we start by analyzing the given nucleus.
Ground State Configuration:
- ( ^7_3\text{Li} ) has ( Z = 3 ) (3 protons) and ( N = 4 ) (4 neutrons).
- In the nuclear shell model, nucleons fill energy levels in the sequence ( 1s_{1/2}, 1p_{3/2}, 1p_{1/2}, \dots ), following the Pauli exclusion principle and spin-orbit coupling.
- The 3 protons fill the levels as follows:
- Two protons occupy the ( 1s_{1/2} ) orbital.
- One proton occupies the ( 1p_{3/2} ) orbital.
- For neutrons (( N = 4 )):
- Two neutrons occupy the ( 1s_{1/2} ) orbital.
- Two neutrons occupy the ( 1p_{3/2} ) orbital.
The ground-state configuration is:
[
(1s_{1/2})^2_p (1p_{3/2})^1_p \quad (1s_{1/2})^2_n (1p_{3/2})^2_n
]
The unpaired proton in the ( 1p_{3/2} ) orbital determines the spin-parity of the nucleus:
[
J^\pi = \frac{3}{2}^-
]
Magnetic Moment:
The magnetic moment is given by:
[
\mu = g_J J
]
For a single proton in ( 1p_{3/2} ), ( g_J = g_l + \frac{g_s – g_l}{2l + 1} ), where ( g_l = 1 ) and ( g_s \approx 5.586 ). For ( l = 1 ) and ( j = \frac{3}{2} ):
[
g_J = 1 + \frac{5.586 – 1}{3} = 2.528
]
Thus:
[
\mu = 2.528 \times \frac{3}{2} = 3.792 \, \mu_N
]
First Excited State:
In the first excited state, a proton is excited from ( 1p_{3/2} ) to ( 1p_{1/2} ). The two most likely configurations are:
- The proton in ( 1p_{3/2} ) moves to ( 1p_{1/2} ), giving ( J^\pi = \frac{1}{2}^- ).
- Another possibility is the excitation to a higher ( p )-shell orbital (e.g., ( 2s_{1/2} )), leading to ( J^\pi = \frac{1}{2}^+ ).
This explains the shell model configuration and its predictions for ( ^7_3\text{Li} ).