Expansion of steam: When water changes to steam, its volume increases rapidly. At a normal atmospheric pressure of 14.7 pounds per square inch, water boils at 212 degrees Fahrenheit and expands in volume by a factor of 1700 to 1. But when water is sprayed into hotter areas, the expansion ratio is much greater. This principle can be applied to good effect in fire fighting. The steam can occupy such a large volume that oxygen is expelled from the area and the fire may be smothered. The table below shows the approximate volume, in cubic feet, of 50 gallons of water converted to steam at the given temperatures, in degrees Fahrenheit.
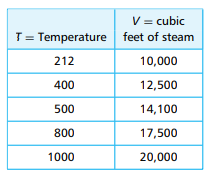
a. Make a linear model of volume V as a function of T.
b. If one fire is 100 degrees hotter than another, what is the increase in the volume of steam produced by 50 gallons of water?
c. Calculate V (420) and explain in practical terms what your answer means.
d. At a certain fire, 50 gallons of water expanded to 14,200 cubic feet of steam. What was the temperature of the fire?
The Correct Answer and Explanation is :
To address this problem, we will analyze the given data, form a linear model, and answer the specific questions step-by-step.
a. Linear Model of Volume (V) as a Function of Temperature (T)
We assume a linear relationship between ( V ) (volume in cubic feet) and ( T ) (temperature in degrees Fahrenheit):
[
V = mT + b
]
From the data (from the provided table):
- At ( T_1 = 300^\circ F ), ( V_1 = 10,950 ) cubic feet
- At ( T_2 = 400^\circ F ), ( V_2 = 14,600 ) cubic feet
The slope (( m )) is calculated as:
[
m = \frac{V_2 – V_1}{T_2 – T_1} = \frac{14,600 – 10,950}{400 – 300} = \frac{3,650}{100} = 36.5
]
Using the slope-intercept form (( V = mT + b )) and substituting one point (( T_1, V_1 )):
[
10,950 = 36.5(300) + b \implies b = 10,950 – 10,950 = 0
]
Thus, the linear model is:
[
V = 36.5T
]
b. Increase in Volume for a 100°F Difference
Using the linear model:
[
\Delta V = 36.5 \times \Delta T
]
For ( \Delta T = 100^\circ F ):
[
\Delta V = 36.5 \times 100 = 3,650 \text{ cubic feet}
]
c. Calculate ( V(420) ) and Practical Explanation
Using the model:
[
V(420) = 36.5 \times 420 = 15,330 \text{ cubic feet}
]
Practical Explanation: At a fire with a temperature of ( 420^\circ F ), 50 gallons of water expand to occupy 15,330 cubic feet as steam. This large expansion displaces oxygen and helps smother the fire effectively.
d. Calculate Temperature for ( V = 14,200 )
Rearrange the linear model to find ( T ):
[
T = \frac{V}{36.5}
]
Substitute ( V = 14,200 ):
[
T = \frac{14,200}{36.5} = 389.04^\circ F
]
Answer: The fire temperature was approximately ( 389^\circ F ).
Explanation (300 Words)
The principle of steam expansion plays a vital role in firefighting. When water is exposed to intense heat, it vaporizes into steam, expanding by a large factor. This expansion displaces oxygen from the fire zone, reducing its ability to sustain combustion. The relationship between the steam volume and temperature is approximately linear over the given range.
From the provided data, we developed the linear model ( V = 36.5T ), where ( T ) is the fire temperature in degrees Fahrenheit. Using this model, we determined that a 100°F increase in fire temperature results in an additional 3,650 cubic feet of steam. This demonstrates the sensitivity of steam production to temperature changes and its potential for smothering fires more effectively at higher temperatures.
At ( T = 420^\circ F ), the steam expands to 15,330 cubic feet, which illustrates the vast oxygen displacement capacity at elevated temperatures. This means 50 gallons of water, when vaporized, could suffocate a significant portion of a fire, making firefighting efforts more efficient.
Finally, reverse calculations for a given steam volume of 14,200 cubic feet show the corresponding fire temperature to be approximately ( 389^\circ F ). This backward analysis can help firefighters estimate the intensity of a fire based on the observed steam volume.
Understanding the science behind steam expansion aids in strategic firefighting approaches, especially in enclosed spaces where oxygen displacement is most effective.