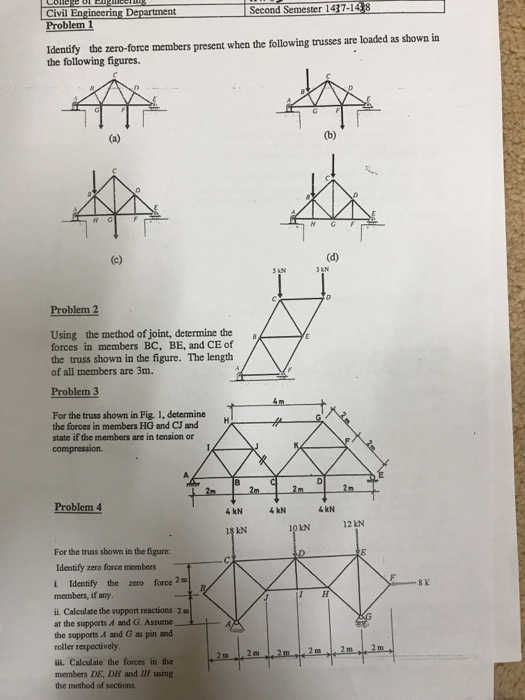
Identify the zero-force members present when the following trusses are loaded as shown in the following figures. Using the method of joint, determine the forces in members BC, BE, and CE of the truss shown in the figure. The length of all members are 3m. For the truss shown in Fig. 1, determine the forces in members HG and CJ and state if the members are in tension or compression. For the truss shown in the figure: Identify zero force members i. Identify the zero force members, if any. ii. Calculate the support reactions at the supports A and G. Assume the supports A and G as pin and roller respectively. iii. Calculate the fortes in the members DE, DH and IH using the method of sections.
The Correct Answer and Explanation is :
To analyze the given trusses, we’ll follow a systematic approach:
- Identify Zero-Force Members: Zero-force members are structural elements in a truss that, under specific loading conditions, carry no tension or compression forces. Recognizing these members simplifies the analysis. The primary rules to identify zero-force members are:
- Rule 1: If two non-collinear members meet at a joint unstressed by external forces or reactions, both are zero-force members.
- Rule 2: If three members form a joint where two are collinear and the joint is free of external forces or reactions, the non-collinear member is a zero-force member. Applying these rules to the provided truss diagrams will help pinpoint the zero-force members.
- Determine Support Reactions at Supports A and G: Assuming support A is a pin (providing both horizontal and vertical reactions) and support G is a roller (providing only a vertical reaction), we can calculate the reactions using static equilibrium equations:
- Sum of Horizontal Forces (ΣFx = 0): Ensures no net horizontal force.
- Sum of Vertical Forces (ΣFy = 0): Ensures no net vertical force.
- Sum of Moments (ΣM = 0): Ensures no net moment about any point. By applying these equations, we can solve for the unknown reactions at supports A and G.
- Calculate Forces in Members DE, DH, and IH Using the Method of Sections: The method of sections involves cutting through the truss to isolate a section and analyzing the forces within that section. The steps are:
- Make an Imaginary Cut: Pass a section through members DE, DH, and IH, ensuring the cut doesn’t pass through more than three members whose forces are unknown.
- Isolate a Section: Choose one side of the cut for analysis.
- Apply Equilibrium Equations: Use ΣFx = 0, ΣFy = 0, and ΣM = 0 to solve for the unknown forces in members DE, DH, and IH. This method simplifies the process by focusing only on the members of interest without analyzing each joint individually.
Explanation:
Identifying zero-force members streamlines the analysis by reducing the number of members to consider, allowing for a more straightforward application of static equilibrium equations. Calculating support reactions is crucial as these reactions influence the internal forces within the truss members. The method of sections is particularly efficient for determining forces in specific members, as it circumvents the need to analyze each joint sequentially. By strategically “cutting” the truss and applying equilibrium equations to the isolated section, we can directly solve for the desired member forces.
This structured approach ensures a comprehensive and efficient analysis of truss structures, facilitating accurate determination of internal forces and identification of zero-force members.