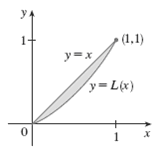
Economists use a cumulative distribution called a Lorenz curve to describe the distribution of income between households in a given country. Typically, a Lorenz curve is defined on [0, 1] with endpoints (0, 0) and (1, 1), and is continuous, increasing, and concave upward. The points on this curve are determined
The Correct Answer and Explanation is :
It seems like you’ve shared a problem related to the Lorenz curve, which is used to measure income inequality. However, the link you provided doesn’t display properly here. If you can describe the problem in detail or provide its mathematical aspects, I can help solve it and provide a detailed explanation.
If the question involves interpreting the Lorenz curve or calculating properties like the Gini coefficient, here’s a general approach:
Explanation of the Lorenz Curve
- Definition:
The Lorenz curve plots the cumulative proportion of income earned by the bottom x% of the population. On the graph:
- The x-axis represents the cumulative percentage of the population (from the poorest to the richest).
- The y-axis represents the cumulative percentage of income.
- Properties:
- It always starts at (0, 0) and ends at (1, 1).
- It is monotonically increasing because adding households cannot decrease cumulative income.
- It is concave upward because wealthier segments typically contribute disproportionately to total income.
- Key Insight:
- A perfectly equal income distribution corresponds to the line of equality: ( y = x ).
- The greater the curvature below this line, the more unequal the income distribution.
- Gini Coefficient:
The Gini coefficient measures income inequality, calculated as:
[
G = \frac{A}{A + B}
]
Where ( A ) is the area between the line of equality and the Lorenz curve, and ( A + B ) is the area under the equality line.
If you describe the exact task or provide numbers/curves, I can calculate specific results or draw a Lorenz curve. Let me know how you’d like to proceed!