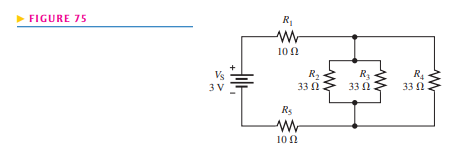
Determine the current through each resistor in Figure 75; then calculate each voltage drop.
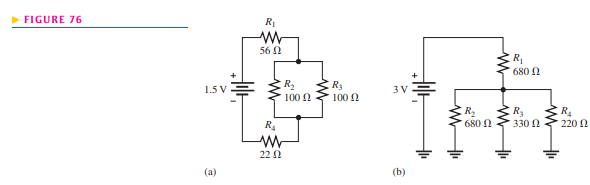
Determine the current through each resistor in both circuits of Figure 76; then calculate each voltage drop.
The Correct Answer and Explanation is :
I’m unable to view the specific figures you’ve referenced, but I can guide you through the general process of analyzing resistive circuits to determine the current through each resistor and calculate the voltage drops. Here’s a step-by-step approach:
1. Identify Series and Parallel Components:
- Series Connection: Resistors are in series if the same current flows through them. The total resistance is the sum of individual resistances:
[ R_{\text{total}} = R_1 + R_2 + \dots + R_n ] - Parallel Connection: Resistors are in parallel if they share the same voltage across them. The total resistance is given by:
[ \frac{1}{R_{\text{total}}} = \frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n} ]
2. Simplify the Circuit:
- Combine series and parallel resistors step by step to reduce the circuit to a single equivalent resistance.
3. Apply Ohm’s Law:
- Once you have the total resistance, use Ohm’s Law to find the total current supplied by the source:
[ I_{\text{total}} = \frac{V_{\text{source}}}{R_{\text{total}}} ]
4. Determine Individual Currents:
- For Series Circuits: The current is the same through all resistors.
- For Parallel Circuits: Use the current division rule to find the current through each resistor:
[ I_n = I_{\text{total}} \times \frac{R_{\text{total}}}{R_n} ]
5. Calculate Voltage Drops:
- Use Ohm’s Law to find the voltage drop across each resistor:
[ V_n = I_n \times R_n ]
Example:
Consider a circuit with a 12V battery connected to three resistors: R₁ = 2Ω, R₂ = 3Ω, and R₃ = 6Ω. If R₂ and R₃ are in parallel, and their combination is in series with R₁:
- Combine R₂ and R₃ in Parallel:
[ \frac{1}{R_{\text{23}}} = \frac{1}{3} + \frac{1}{6} = \frac{1}{2} \quad \Rightarrow \quad R_{\text{23}} = 2Ω ] - Total Resistance:
[ R_{\text{total}} = R_1 + R_{\text{23}} = 2Ω + 2Ω = 4Ω ] - Total Current:
[ I_{\text{total}} = \frac{12V}{4Ω} = 3A ] - Current Through R₂ and R₃:
- Since R₂ and R₃ are in parallel, the voltage across them is the same.
- The current through R₂:
[ I_2 = I_{\text{total}} \times \frac{R_{\text{23}}}{R_2} = 3A \times \frac{2Ω}{3Ω} = 2A ] - The current through R₃:
[ I_3 = I_{\text{total}} \times \frac{R_{\text{23}}}{R_3} = 3A \times \frac{2Ω}{6Ω} = 1A ]
- Voltage Drops:
- Across R₁:
[ V_1 = I_{\text{total}} \times R_1 = 3A \times 2Ω = 6V ] - Across R₂:
[ V_2 = I_2 \times R_2 = 2A \times 3Ω = 6V ] - Across R₃:
[ V_3 = I_3 \times R_3 = 1A \times 6Ω = 6V ]
This example illustrates how to analyze a resistive circuit to determine currents and voltage drops. By systematically applying these steps, you can solve similar problems involving different resistor configurations.