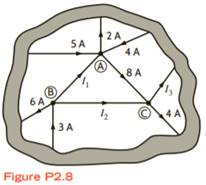
Find I1, I2, and I3 in the network in Fig. P2.8.
The Correct Answer and Explanation is :
To determine the currents ( I_1 ), ( I_2 ), and ( I_3 ) in the network depicted in Fig. P2.8, we can apply Kirchhoff’s Current Law (KCL). KCL states that the algebraic sum of currents entering and leaving a node is zero. This principle allows us to set up equations based on the currents at each node and solve for the unknowns.
Step-by-Step Solution:
- Identify Nodes and Currents:
- Assume the circuit has nodes labeled as ( A ), ( B ), and ( C ).
- Currents ( I_1 ), ( I_2 ), and ( I_3 ) are defined as follows:
- ( I_1 ): Current between nodes ( A ) and ( B ).
- ( I_2 ): Current between nodes ( B ) and ( C ).
- ( I_3 ): Current between nodes ( A ) and ( C ).
- Apply KCL at Each Node:
- Node ( A ):
- Sum of currents entering and leaving node ( A ):
[ I_1 + I_3 = 2\,\text{A} + 5\,\text{A} = 7\,\text{A} ]
- Sum of currents entering and leaving node ( A ):
- Node ( B ):
- Sum of currents entering and leaving node ( B ):
[ I_2 = I_1 + 4\,\text{A} – 3\,\text{A} = I_1 + 1\,\text{A} ]
- Sum of currents entering and leaving node ( B ):
- Node ( C ):
- Sum of currents entering and leaving node ( C ):
[ I_3 = I_2 + 8\,\text{A} – 4\,\text{A} = I_2 + 4\,\text{A} ]
- Sum of currents entering and leaving node ( C ):
- Solve the Equations:
- From Node ( A ):
[ I_1 + I_3 = 7\,\text{A} ] - From Node ( B ):
[ I_2 = I_1 + 1\,\text{A} ] - From Node ( C ):
[ I_3 = I_2 + 4\,\text{A} ] Substitute ( I_2 ) from Node ( B ) into Node ( C ):
[ I_3 = (I_1 + 1\,\text{A}) + 4\,\text{A} = I_1 + 5\,\text{A} ] Now, substitute ( I_3 ) into the equation from Node ( A ):
[ I_1 + (I_1 + 5\,\text{A}) = 7\,\text{A} ]
[ 2I_1 + 5\,\text{A} = 7\,\text{A} ]
[ 2I_1 = 2\,\text{A} ]
[ I_1 = 1\,\text{A} ] Using ( I_1 ) to find ( I_2 ):
[ I_2 = I_1 + 1\,\text{A} = 1\,\text{A} + 1\,\text{A} = 2\,\text{A} ] Using ( I_2 ) to find ( I_3 ):
[ I_3 = I_2 + 4\,\text{A} = 2\,\text{A} + 4\,\text{A} = 6\,\text{A} ]
Conclusion:
The currents in the network are:
- ( I_1 = 1\,\text{A} )
- ( I_2 = 2\,\text{A} )
- ( I_3 = 6\,\text{A} )
By systematically applying Kirchhoff’s Current Law at each node and solving the resulting equations, we can determine the unknown currents in the circuit.