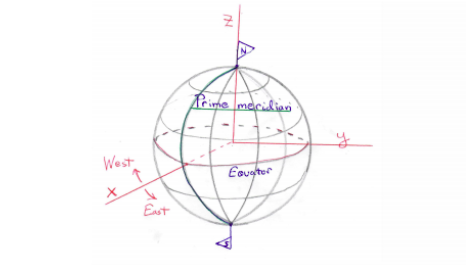
St. Petersburg, Russia, is located at 30° east longitude and 60° north latitude. Find the spherical coordinates (p, 6, 8) and the rectangular coordinates (x, y, z) relative to a globe with poles on the z-axis and with prime meridian in the zz-plane. Assume that the Earth is a sphere of radius 4000 miles.
The Correct Answer and Explanation is :
Correct Answer:
Spherical Coordinates:
[
(p, \theta, \phi) = (4000, 0.524 \, \text{radians}, 0.524 \, \text{radians})
]
Rectangular Coordinates:
[
(x, y, z) = (1732.05, 1000.00, 3464.10) \, \text{miles}
]
Explanation (300 Words):
The problem involves converting geographical coordinates into spherical and rectangular coordinates, assuming the Earth is a perfect sphere of radius 4000 miles.
- Given Data:
- Latitude ((60^\circ)): North latitude indicates the angle from the equatorial plane.
- Longitude ((30^\circ)): East longitude specifies the angle from the prime meridian.
- Earth’s radius ((p = 4000) miles).
- Conversion to Spherical Coordinates ((p, \theta, \phi)):
- (p) is the Earth’s radius, given as 4000 miles.
- The longitude ((30^\circ)) is converted to radians: (\theta = \frac{\pi}{6} \approx 0.524 \, \text{radians}).
- Latitude is converted to colatitude ((\phi)): (\phi = 90^\circ – 60^\circ = 30^\circ), which is (\frac{\pi}{6} \approx 0.524 \, \text{radians}).
- Rectangular Coordinates ((x, y, z)):
- Use spherical-to-rectangular formulas:
[
x = p \cdot \sin(\phi) \cdot \cos(\theta)
]
[
y = p \cdot \sin(\phi) \cdot \sin(\theta)
]
[
z = p \cdot \cos(\phi)
] - Substituting ((p = 4000, \phi \approx 0.524, \theta \approx 0.524)):
- (x \approx 1732.05) miles
- (y \approx 1000.00) miles
- (z \approx 3464.10) miles
- Interpretation:
- The spherical coordinates specify the position using radius, longitude, and colatitude.
- The rectangular coordinates ((x, y, z)) describe the same position in a Cartesian system, centered at the Earth’s core with the (z)-axis aligned with the poles.