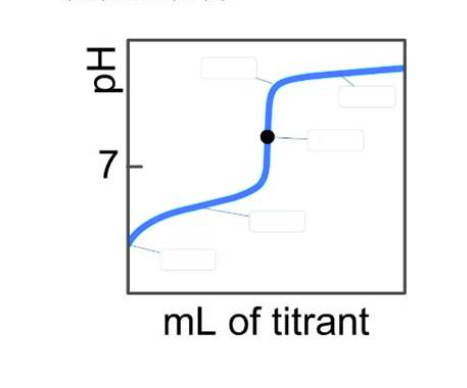
On the weak acid/strong base titration curve below, label the following points. a) The point where the pH corresponds to a solution of the weak acid (HA) in water. b) The point where the pH corresponds to a solution of the conjugate base (A) in water. c) The point where pH = pK.
The Correct Answer and Explanation is :
In a titration of a weak acid (HA) with a strong base, the pH changes as the base is added. The points of interest on the titration curve are:
a) The point where the pH corresponds to a solution of the weak acid (HA) in water:
At the start of the titration, before any base is added, the solution contains only the weak acid (HA) dissolved in water. The pH at this point is determined by the dissociation of the weak acid in water, which is characterized by its acid dissociation constant (Ka). The pH can be calculated using the formula:
pH=12(pKa−log[HA])\text{pH} = \frac{1}{2} \left( \text{pKa} – \log [\text{HA}] \right)
where pKa is the negative logarithm of Ka, and [HA] is the concentration of the weak acid. This point is at the very beginning of the titration curve.
b) The point where the pH corresponds to a solution of the conjugate base (A⁻) in water:
After adding a sufficient amount of the strong base, the weak acid is neutralized, and the solution contains the conjugate base (A⁻) of the weak acid. The pH at this point is determined by the hydrolysis of the conjugate base in water, which is characterized by its base dissociation constant (Kb). The pH can be calculated using the formula:
pH=14−12(pKb−log[A−])\text{pH} = 14 – \frac{1}{2} \left( \text{pKb} – \log [\text{A}^-] \right)
where pKb is the negative logarithm of Kb, and [A⁻] is the concentration of the conjugate base. This point is reached after the equivalence point on the titration curve.
c) The point where pH = pKa:
The pH equals the pKa of the weak acid at the half-equivalence point of the titration. At this stage, half of the weak acid has been neutralized by the strong base, resulting in equal concentrations of the weak acid (HA) and its conjugate base (A⁻). The pH at this point can be calculated using the Henderson-Hasselbalch equation:
pH=pKa+log([A−][HA])\text{pH} = \text{pKa} + \log \left( \frac{[\text{A}^-]}{[\text{HA}]} \right)
Since [A⁻] = [HA] at the half-equivalence point, the equation simplifies to:
pH=pKa\text{pH} = \text{pKa}
This point is typically located at the midpoint of the steep rise in the titration curve.
Understanding these points is crucial for interpreting titration curves and determining the pKa of weak acids. The initial pH reflects the weak acid’s dissociation in water, the half-equivalence point indicates the pKa, and the final pH corresponds to the behavior of the conjugate base in water. These concepts are fundamental in acid-base chemistry and are essential for analyzing titration data.