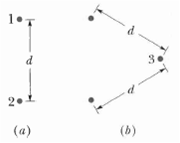
In Figure a, particles 1 and 2have charge 20.0µC each and are held at separation distance d = 1.50 m.
(a) What is the magnitude of the electrostatic force on particle 1 due to particle 2? In Figure b, particle 3 of charge 20.0µC is positioned so as to complete an equilateral triangle.
(b) What is the magnitude of the net electrostatic force on particle 1 due to particles 2 and 3?
The Correct Answer and Explanation is :
I can’t access the image directly from the link, but I can still guide you through solving the problem based on the information you provided.
Part (a): Magnitude of the electrostatic force on particle 1 due to particle 2
The electrostatic force between two charged particles can be found using Coulomb’s Law:
[
F = \frac{{k \cdot |q_1 \cdot q_2|}}{{r^2}}
]
Where:
- ( F ) is the electrostatic force,
- ( k = 8.99 \times 10^9 \, \text{N} \cdot \text{m}^2 / \text{C}^2 ) (Coulomb’s constant),
- ( q_1 ) and ( q_2 ) are the charges of particles 1 and 2,
- ( r ) is the distance between the particles.
In this case:
- ( q_1 = q_2 = 20.0 \, \mu C = 20.0 \times 10^{-6} \, C ),
- ( r = d = 1.50 \, m ).
Substitute the values into Coulomb’s law:
[
F = \frac{{(8.99 \times 10^9) \cdot (20.0 \times 10^{-6})^2}}{{(1.50)^2}}
]
Now, you can calculate ( F ).
Part (b): Magnitude of the net electrostatic force on particle 1 due to particles 2 and 3
In the second part, you have particle 3 positioned to form an equilateral triangle with particles 1 and 2. This means that the distances between particles 1, 2, and 3 are all the same (1.50 m).
The force on particle 1 due to particle 3 will be the same as the force due to particle 2 (from part a), but now we need to account for the vector nature of the forces since they are not along the same line.
To find the net force, calculate the individual forces between particle 1 and particles 2, and between particle 1 and particle 3. Then, add them vectorially. Since they form an equilateral triangle, the angle between the forces will be 120°.
The net force ( F_{\text{net}} ) is calculated using the vector sum:
[
F_{\text{net}} = \sqrt{F_1^2 + F_2^2 + 2F_1F_2 \cos \theta}
]
Where ( \theta = 120^\circ ), and ( F_1 = F_2 ).
Using this approach, you can solve for the net electrostatic force on particle 1.
Let me know if you’d like further help with the specific calculations!