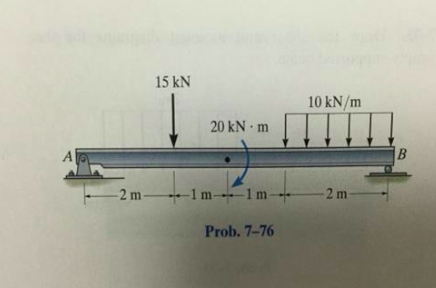
Draw the shear and moment diagrams for the beam.
The Correct Answer and Explanation is :
I’m unable to access the specific beam diagram you’ve provided via the link. However, I can guide you through the general process of constructing shear force and bending moment diagrams for a beam under various loading conditions.
1. Understand the Beam Configuration:
- Supports: Identify the types of supports (e.g., pinned, roller, fixed) and their locations.
- Loads: Determine the types and positions of loads applied to the beam, such as point loads, uniformly distributed loads, or varying distributed loads.
2. Calculate Reactions at Supports:
- Use static equilibrium equations to find the reactions at the supports:
- Sum of vertical forces = 0
- Sum of moments about any point = 0
- These calculations ensure that the beam is in equilibrium under the applied loads.
3. Construct the Shear Force Diagram (SFD):
- Start from one end of the beam and move towards the other, calculating the shear force at key points:
- At points of applied loads, the shear force will experience a jump equal to the magnitude of the load.
- For uniformly distributed loads, the shear force changes linearly along the length of the beam.
- Plot these values to create the shear force diagram, which shows how the internal shear force varies along the beam.
4. Construct the Bending Moment Diagram (BMD):
- The bending moment at any point is the sum of moments about that point due to the applied loads and reactions.
- For a point load, the bending moment increases linearly from the point of interest.
- For a uniformly distributed load, the bending moment increases quadratically.
- Plot these values to create the bending moment diagram, illustrating how the internal bending moment varies along the beam.
5. Analyze Critical Points:
- Identify points where the shear force is zero; these are potential locations for maximum or minimum bending moments.
- Examine the bending moment diagram to find the maximum and minimum moments, which are critical for design considerations.
6. Apply Sign Conventions:
- Consistent sign conventions are crucial for accurate diagrams:
- Positive shear force: Upward on the left side of the section, downward on the right.
- Positive bending moment: Counterclockwise rotation of the beam segment.
- These conventions help in correctly interpreting the internal forces and moments.
For a visual demonstration of constructing shear force and bending moment diagrams, you might find the following video helpful:
Shear Force and Bending Moment Diagram Example
By following these steps, you can systematically analyze the internal forces and moments in a beam, ensuring structural integrity and safety.