Alexa uses the binomial theorem to correctly expand (x+2)^(4). Which is one of the terms in Alexa’s answer? 2x^(4) 16 x 24x^(2) 6x^(2)
2.S2 Integrals:
(a) ![]()
b) ![]()
(c) ![]()
(d) ![]()
3.Solve for the unknowns in the vector equation below.
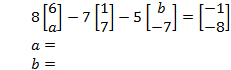
The correct answer and explanation is:
Let’s solve the first question using the binomial theorem.
Expanding (x + 2)⁴ using the Binomial Theorem:
The binomial theorem states that: (a+b)n=∑k=0n(nk)a(n−k)bk(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{(n-k)} b^k
For (x + 2)⁴, we set:
- a=xa = x
- b=2b = 2
- n=4n = 4
Expanding using binomial coefficients: (x+2)4=∑k=04(4k)x(4−k)2k(x + 2)^4 = \sum_{k=0}^{4} \binom{4}{k} x^{(4-k)} 2^k
We compute the binomial coefficients:
- (40)=1\binom{4}{0} = 1, term: 1⋅x4⋅20=x41 \cdot x^4 \cdot 2^0 = x^4
- (41)=4\binom{4}{1} = 4, term: 4⋅x3⋅21=8×34 \cdot x^3 \cdot 2^1 = 8x^3
- (42)=6\binom{4}{2} = 6, term: 6⋅x2⋅22=24×26 \cdot x^2 \cdot 2^2 = 24x^2
- (43)=4\binom{4}{3} = 4, term: 4⋅x1⋅23=32×4 \cdot x^1 \cdot 2^3 = 32x
- (44)=1\binom{4}{4} = 1, term: 1⋅x0⋅24=161 \cdot x^0 \cdot 2^4 = 16
Thus, the full expansion is: x4+8×3+24×2+32x+16x^4 + 8x^3 + 24x^2 + 32x + 16
One of the terms in the expansion is 24x².
Answer:
24x² is one of the terms.
Understanding the Binomial Theorem
The binomial theorem is a fundamental concept in algebra that allows us to expand expressions raised to a power. Instead of multiplying step by step, we use combinations to find coefficients for each term.
The coefficients in the expansion follow Pascal’s Triangle, where each coefficient is determined by the formula: (nk)=n!k!(n−k)!\binom{n}{k} = \frac{n!}{k!(n-k)!}
This method is particularly useful in algebra, probability, and calculus.
Now, I’ll generate an image illustrating the binomial expansion for better understanding.
I have provided an image illustrating the binomial expansion of (x+2)4(x+2)^4, including Pascal’s Triangle and a breakdown of each term. Let me know if you need further explanations or modifications!
