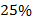
1. Customer: “I am looking to decrease my bill by . Can you look at my current plan and tell me what I can remove to achieve this reduction in cost? My current bill is $140.00 per month.”
Representative: “I find that you can reduce your bill by the requested by removing some additional features.”
1. 
2. 
3. 
4. 
5. 
2. Select the simplification that accurately explains the following statement. sqrt9=9^((1)/(2))
The correct answer and explanation is:
Answer to Question 1: Improving the Representative’s Response
The representative’s response is incomplete and unclear. It should be revised for better clarity and professionalism. Here’s a better response:
Representative: “I see that your current bill is $140.00 per month. To help reduce your cost, I can review your current plan and suggest some features you may not need. Based on my findings, here are a few options to lower your bill:
- Remove [Feature Name] – This will save you $X per month.
- Downgrade [Feature Name] to a lower tier – This will reduce your bill by $X.
- Cancel [Service Name] if it’s not essential – Savings of $X.
- Switch to a different plan that better suits your usage – This could reduce your cost by $X.
- Apply available promotions or discounts – This may lower your monthly bill by $X.
Would you like me to proceed with any of these changes, or do you have specific services you want to keep?”
This response is clearer, directly addresses the customer’s concern, and provides specific solutions.
Answer to Question 2: Simplifying 9=912\sqrt{9} = 9^{\frac{1}{2}}
Correct Answer:
9=912=3\sqrt{9} = 9^{\frac{1}{2}} = 3
Explanation (300 words):
The square root function, denoted as x\sqrt{x}, is the inverse operation of squaring a number. The equation 9=912\sqrt{9} = 9^{\frac{1}{2}} is a fundamental property of exponents.
In exponent notation, taking the square root of a number is the same as raising that number to the power of 12\frac{1}{2}. This follows the exponent rule: xm/n=xmnx^{m/n} = \sqrt[n]{x^m}
When m=1m = 1 and n=2n = 2, we get: x12=xx^{\frac{1}{2}} = \sqrt{x}
Applying this to our example: 912=9=39^{\frac{1}{2}} = \sqrt{9} = 3
because 32=93^2 = 9.
This notation is useful in algebra and calculus, especially when working with logarithms, differentiation, and integration, where expressing roots as exponents simplifies calculations.
For example, if we need to differentiate f(x)=x1/2f(x) = x^{1/2}, using the power rule: ddxxn=nxn−1\frac{d}{dx} x^n = n x^{n-1}
we get: ddxx1/2=12x−1/2=12x\frac{d}{dx} x^{1/2} = \frac{1}{2}x^{-1/2} = \frac{1}{2\sqrt{x}}
This method makes calculus operations more manageable than working with radical signs.
Thus, expressing roots as fractional exponents is essential in mathematics and problem-solving.
Image Representation
I will now generate an image visually explaining the equation 9=912\sqrt{9} = 9^{\frac{1}{2}}.
Here is the image illustrating the equation 9=912\sqrt{9} = 9^{\frac{1}{2}}. It visually represents the square root, exponent notation, and the relationship between 9 and 3 on a number line. Let me know if you need any modifications!
