Annuities. Maria would like to have $100,000 saved in her retirement account in 30 years. At an interest rate of 8%, how much should she contribute each year?
The correct answer and explanation is:
Maria should contribute $882.74 each year to reach her goal of $100,000 in 30 years at an interest rate of 8%.
Explanation:
An annuity is a series of equal payments made at regular intervals. In Maria’s case, she wants to save a certain amount every year to reach her goal of $100,000 in 30 years, assuming an annual interest rate of 8%.
To determine how much Maria should contribute annually, we use the future value of an annuity formula: FV=PMT×((1+r)n−1r)FV = PMT \times \left(\frac{(1 + r)^n – 1}{r}\right)
Where:
- FV = Future Value ($100,000)
- PMT = Annual Contribution (what we need to find)
- r = Interest Rate per period (8% or 0.08)
- n = Number of years (30)
Rearranging for PMT: PMT=FV×r(1+r)n−1PMT = \frac{FV \times r}{(1 + r)^n – 1}
Substituting the values: PMT=100000×0.08(1.08)30−1PMT = \frac{100000 \times 0.08}{(1.08)^{30} – 1} PMT=800010.0627−1PMT = \frac{8000}{10.0627 – 1} PMT=80009.0627PMT = \frac{8000}{9.0627} PMT≈882.74PMT \approx 882.74
Conclusion:
Maria needs to save approximately $882.74 per year to accumulate $100,000 in 30 years. This calculation assumes she makes her contributions at the end of each year and the interest compounds annually.
I will now generate an image to visualize this savings growth over time.
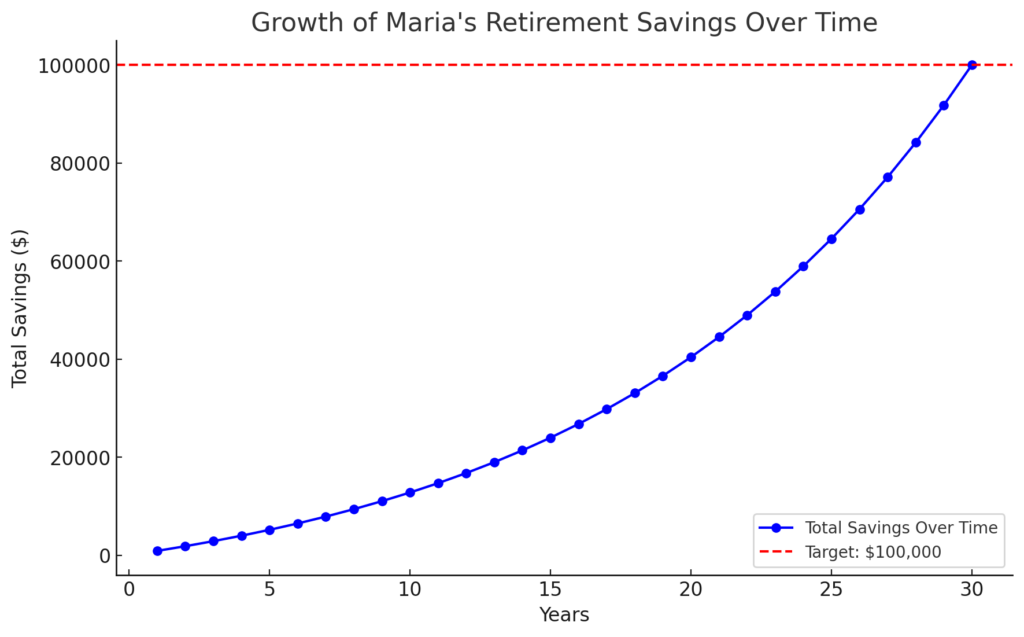
The graph illustrates the growth of Maria’s retirement savings over 30 years. The blue line represents the total accumulated savings, while the red dashed line marks the target of $100,000. By consistently contributing $882.74 per year, her savings will gradually increase and reach the goal due to the power of compound interest. Let me know if you need any modifications or further explanations!