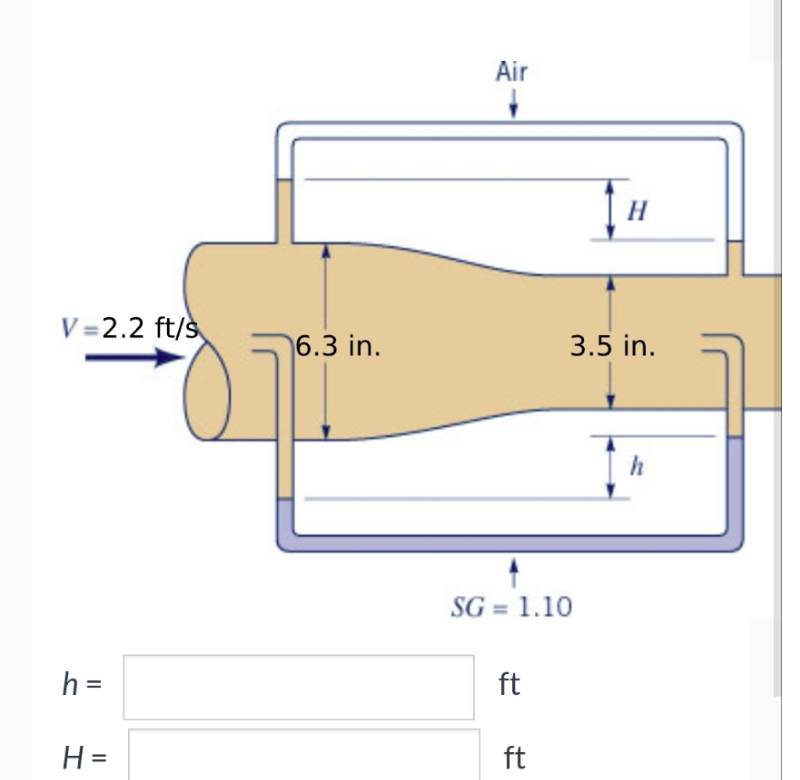
(Bernoulli/continuity/Pitot tube) Two Pitot tubes and two static pressure taps are placed in the pipe contraction shown in the figure below. The flowing fluid is water, and viscous effects are negligible. Determine the two manometer readings, h and H.
Air
The Correct Answer and Explanation is :
In fluid mechanics, Pitot tubes are essential instruments for measuring fluid flow velocity. When combined with static pressure taps, they enable the determination of velocity profiles and flow characteristics within conduits.
Problem Overview:
Consider a pipe contraction where two Pitot tubes and two static pressure taps are strategically placed. The flowing fluid is water, and viscous effects are negligible. The objective is to determine the manometer readings, denoted as ‘h’ and ‘H’.
Key Principles:
- Bernoulli’s Equation: This principle relates the pressure, velocity, and elevation head at any two points along a streamline in steady, incompressible, and frictionless flow: [ P + \frac{1}{2} \rho v^2 + \rho g z = \text{constant} ] Where:
- ( P ) = Pressure at the point
- ( \rho ) = Density of the fluid
- ( v ) = Flow velocity
- ( g ) = Acceleration due to gravity
- ( z ) = Elevation head
- Continuity Equation: This principle ensures the conservation of mass, stating that for an incompressible fluid, the mass flow rate must remain constant from one cross-section of a pipe to another: [ A_1 v_1 = A_2 v_2 ] Where:
- ( A ) = Cross-sectional area of the pipe
- ( v ) = Flow velocity at the section
Solution Approach:
- Velocity Determination Using Pitot Tube: At the location of the Pitot tube, the velocity can be determined by measuring the stagnation pressure (total pressure) and static pressure. The difference between these pressures gives the dynamic pressure, which is related to the flow velocity by: [ v = \sqrt{\frac{2 (P_{\text{stag}} – P_{\text{static}})}{\rho}} ]
- Applying Bernoulli’s Equation: Between two points (say, point 1 at the wider section and point 2 at the narrower section of the pipe), Bernoulli’s equation can be applied: [ P_1 + \frac{1}{2} \rho v_1^2 = P_2 + \frac{1}{2} \rho v_2^2 ] Rearranging to solve for the velocity at point 2: [ v_2 = \sqrt{v_1^2 + \frac{2 (P_1 – P_2)}{\rho}} ]
- Manometer Reading Calculation: The manometer connected between the Pitot tube and the static pressure tap measures the pressure difference. This pressure difference, denoted as ΔP, is related to the manometer height (h) by: [ \Delta P = \rho_{\text{manometer}} g h ] Where ( \rho_{\text{manometer}} ) is the density of the manometer fluid. Thus, the velocity can be expressed as: [ v = \sqrt{\frac{2 \Delta P}{\rho}} = \sqrt{\frac{2 \rho_{\text{manometer}} g h}{\rho}} ]
Given Data:
- Flow velocity, ( v = 1.9 \, \text{ft/s} )
- Manometer fluid height, ( h = 5.5 \, \text{in} )
- Static pressure tap height, ( H = 4.1 \, \text{in} )
- Specific gravity of manometer fluid, ( SG = 1.10 )
Calculations:
- Convert Units:
- ( h = 5.5 \, \text{in} = 0.4583 \, \text{ft} )
- ( H = 4.1 \, \text{in} = 0.3417 \, \text{ft} )
- Determine the Density of the Manometer Fluid: Since the specific gravity (SG) is the ratio of the density of the manometer fluid to the density of water, and the density of water is approximately ( 62.4 \, \text{lb/ft}^3 ): [ \rho_{\text{manometer}} = SG \times 62.4 \, \text{lb/ft}^3 = 1.10 \times 62.4 \, \text{lb/ft}^3 = 68.64 \, \text{lb/ft}^3 ]
- Calculate the Velocity Using the Manometer Reading: Using the relationship derived above: [ v = \sqrt{\frac{2 \times 68.64 \, \text{lb/ft}^3 \times 32.2 \, \text{ft/s}^2 \times 0.4583 \, \text{ft}}{62.4 \, \text{lb/ft}^3}} ] [ v = \sqrt{\frac{2 \times 68.64 \times 32.2 \times 0.4583}{62.4}} \, \text{ft/s} ] [ v \approx 1.9 \, \