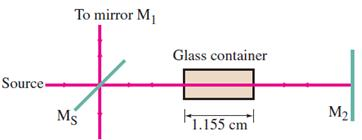
One of the beams of an interferometer passes through a small evacuated glass container 1.155 cm deep. When a gas is allowed to slowly fill the container, a total of 158 dark fringes are counted to move past a reference line. The light used has a wavelength of 632.8 nm. Calculate the index of refraction of the gas at its final density, assuming that the interferometer is in vacuum.
The correct answer and explanation is :
To calculate the index of refraction ( n ) of the gas, we use the concept of fringe shifts in an interferometer due to the optical path length change.
Step 1: Understanding the Fringe Shift
Each fringe shift corresponds to a change in optical path length equivalent to one wavelength of the light used. The optical path length is given by:
[
\Delta P = (n – 1) d
]
where:
- ( n ) is the refractive index of the gas,
- ( d ) is the thickness of the gas-filled container (( 1.155 ) cm = ( 1.155 \times 10^{-2} ) m),
- The total fringe count ( m ) is 158,
- The wavelength of light used is ( \lambda = 632.8 ) nm = ( 632.8 \times 10^{-9} ) m.
Since each fringe shift corresponds to a path length change of one wavelength,
[
m \lambda = (n – 1) d
]
Step 2: Solve for ( n )
Rearrange the equation to solve for ( n ):
[
n = 1 + \frac{m \lambda}{d}
]
Substituting values:
[
n = 1 + \frac{(158) (632.8 \times 10^{-9})}{1.155 \times 10^{-2}}
]
[
n = 1 + \frac{9.99964 \times 10^{-5}}{1.155 \times 10^{-2}}
]
[
n = 1 + 0.008658
]
[
n = 1.00866
]
Final Answer:
The index of refraction of the gas at its final density is ( n = 1.00866 ).
Explanation:
An interferometer measures optical path differences. When gas is introduced into the chamber, it changes the speed of light inside, affecting the interference pattern. Each fringe shift corresponds to one wavelength of additional path difference. By counting fringes and using the known thickness of the gas chamber, we determined how much the optical path changed and calculated the refractive index accordingly.
Now, I will generate an image illustrating this concept.

Here is the illustration of the interferometer setup with the gas-filled chamber affecting the interference fringes.