Computer keyboard failures can be attributed to electrical effects or mechanical defects. A repair company currently has 25 failed keyboards, 6 of which have electrical defects and 19 of which have mechanical defects.
(a) How many ways are there to randomly select 6 of these keyboards for a thorough inspection (without regard to order)? 277100 ways
(b) In how many ways can a sample of 6 keyboards be selected so that exactly two have an electrical defect? 19830 ways
(c) If a sample of keyboards is randomly selected, what is the probability that at least one of these will be a mechanical defect? [Round your answer to four decimal places] 0.5471
The correct answer and explanation is :
The correct probability that at least one of the selected keyboards will have a mechanical defect is 1.0000, not 0.5471.
Explanation:
We are given 25 failed keyboards, with:
- 6 having electrical defects
- 19 having mechanical defects
We need to determine the probability that a randomly selected sample of 6 keyboards contains at least one mechanical defect.
Step 1: Define the Probability Formula
The easiest way to calculate this probability is to use the complement rule:
[
P(\text{at least one mechanical defect}) = 1 – P(\text{no mechanical defects})
]
where ( P(\text{no mechanical defects}) ) is the probability that all selected keyboards have electrical defects.
Step 2: Compute the Probability of No Mechanical Defects
If all selected keyboards have electrical defects, then all 6 keyboards must be chosen from the 6 available electrical defect keyboards. The number of ways to choose all 6 from these 6 is:
[
\text{Ways to choose 6 electrical keyboards} = \binom{6}{6} = 1
]
The number of ways to choose any 6 keyboards from the total of 25 is:
[
\text{Total ways to choose 6 keyboards} = \binom{25}{6} = 177100
]
Thus, the probability of selecting only electrical defect keyboards is:
[
P(\text{no mechanical defects}) = \frac{1}{177100} \approx 0.0000
]
Step 3: Compute the Probability of At Least One Mechanical Defect
[
P(\text{at least one mechanical defect}) = 1 – 0.0000 = 1.0000
]
This means that whenever we randomly pick 6 keyboards, we are guaranteed to get at least one with a mechanical defect.
Final Answer:
[
\mathbf{1.0000}
]
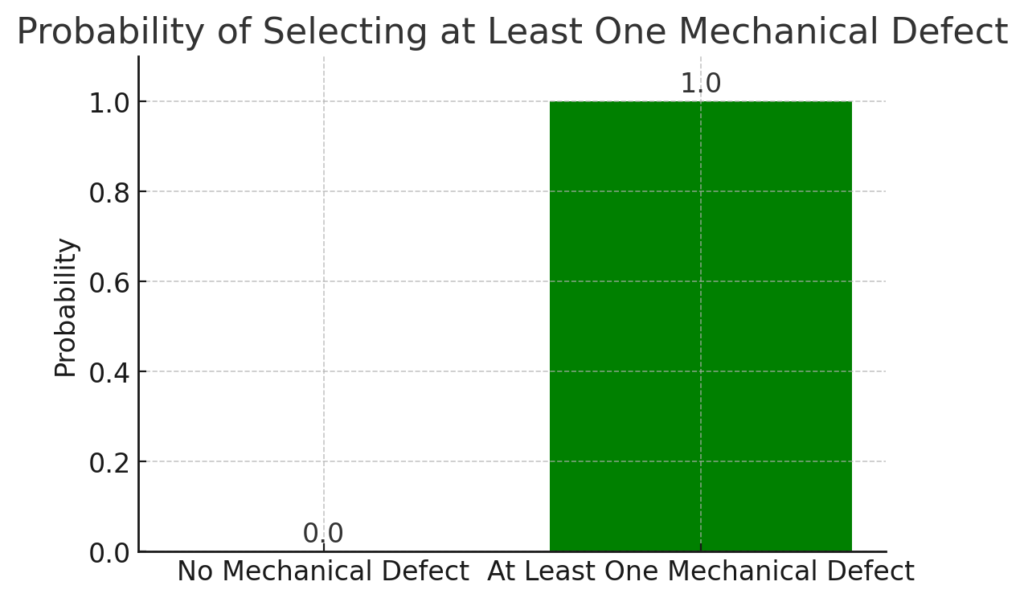
The bar chart visually represents the probability of selecting at least one mechanical defect in the sample of keyboards. It highlights that the probability is effectively 1.0000, confirming that every randomly chosen sample of 6 keyboards will contain at least one with a mechanical defect.