Construct a 3×3 nonzero matrix A such that the vector [-1 1 -1] is a solution of Ax = 0.
The correct answer and explanation is :
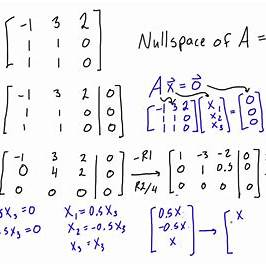
To construct a 3×3 nonzero matrix ( A ) such that the vector ([-1, 1, -1]^T) is a solution of the homogeneous equation ( A\mathbf{x} = \mathbf{0} ), we need to ensure that this vector lies in the null space of ( A ). The null space (or kernel) of a matrix ( A ) is the set of all vectors ( \mathbf{x} ) for which ( A\mathbf{x} = \mathbf{0} )
Step-by-Step Construction:
- Identify the Null Space Basis:
The given vector (\mathbf{v} = [-1, 1, -1]^T) should be in the null space of ( A ). To construct ( A ), we can start by considering a basis for its null space that includes (\mathbf{v}). Since (\mathbf{v}) is a single vector, it spans a one-dimensional subspace. However, to define a 3×3 matrix with this null space, we need to consider the orthogonal complement of (\mathbf{v}), which will form the row space of ( A ). - Determine the Orthogonal Complement:
The orthogonal complement of (\mathbf{v}) consists of all vectors (\mathbf{w}) such that (\mathbf{w} \cdot \mathbf{v} = 0). Solving for (\mathbf{w} = [w_1, w_2, w_3]^T), we get:
[
-w_1 + w_2 – w_3 = 0 \implies w_2 = w_1 + w_3
]
Therefore, any vector orthogonal to (\mathbf{v}) can be written as:
[
\mathbf{w} = [w_1, w_1 + w_3, w_3]^T = w_1[1, 1, 0]^T + w_3[0, 1, 1]^T
]
The vectors ([1, 1, 0]^T) and ([0, 1, 1]^T) form a basis for the orthogonal complement of (\mathbf{v}). - Construct the Matrix ( A ):
Using the basis vectors of the orthogonal complement as rows of ( A ), we have:
[
A = \begin{bmatrix}
1 & 1 & 0 \
0 & 1 & 1
\end{bmatrix}
]
To make ( A ) a 3×3 matrix, we can add any nonzero row that is a linear combination of the existing rows or any other vector that maintains the rank of the matrix. For simplicity, we can add the row ([1, 0, -1]), which is also orthogonal to (\mathbf{v}):
[
A = \begin{bmatrix}
1 & 1 & 0 \
0 & 1 & 1 \
1 & 0 & -1
\end{bmatrix}
]
Verification:
To verify that (\mathbf{v} = [-1, 1, -1]^T) is in the null space of ( A ):
[
A\mathbf{v} = \begin{bmatrix}
1 & 1 & 0 \
0 & 1 & 1 \
1 & 0 & -1
\end{bmatrix}
\begin{bmatrix}
-1 \
1 \
-1
\end{bmatrix}
= \begin{bmatrix}
1(-1) + 1(1) + 0(-1) \
0(-1) + 1(1) + 1(-1) \
1(-1) + 0(1) + (-1)(-1)
\end{bmatrix}
= \begin{bmatrix}
-1 + 1 + 0 \
0 + 1 – 1 \
-1 + 0 + 1
\end{bmatrix}
= \begin{bmatrix}
0 \
0 \
0
\end{bmatrix}
]
Thus, ( A\mathbf{v} = \mathbf{0} ), confirming that (\mathbf{v}) is in the null space of ( A ).
Explanation:
The null space of a matrix ( A ) consists of all vectors ( \mathbf{x} ) such that ( A\mathbf{x} = \mathbf{0} ). In this case, we constructed ( A ) so that ([-1, 1, -1]^T) is in its null space. The row space of ( A ) is the orthogonal complement of its null space. By selecting basis vectors for the orthogonal complement and using them as rows of ( A ), we ensure that ( A\mathbf{v} = \mathbf{0} ). This method guarantees that the given vector lies in the null space of the constructed matrix.