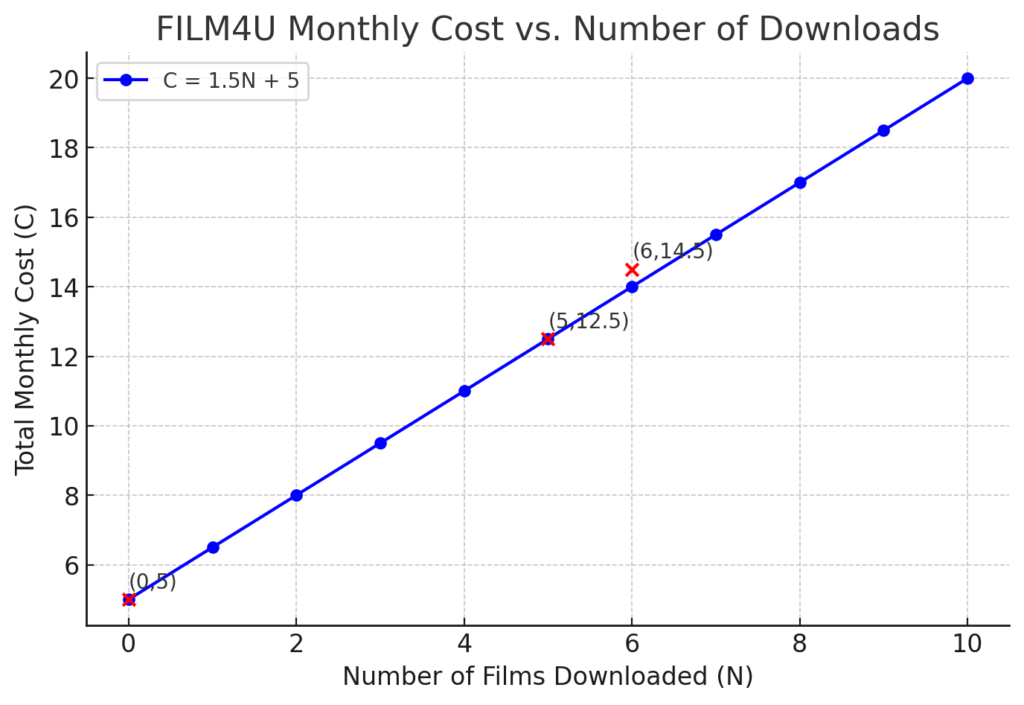
An on-demand company, FILM4U, charges a monthly subscription as well as a fixed cost per download. A graph of the total monthly cost, C,plotted against the number of films, N, downloaded is shown.
(a) Find the price of (i) the monthly subscription and (ii) the unit cost per film.
(b) If my monthly bill is $14.5 how many films did I watch?
The correct answer and explanation is :
To analyze FILM4U’s pricing structure, we can model the total monthly cost ( C ) as a linear function of the number of films downloaded ( N ):
[ C = mN + b ]
Here, ( m ) represents the unit cost per film, and ( b ) denotes the monthly subscription fee.
(a) Determining the Pricing Components:
To find the values of ( m ) and ( b ), we need two data points from the graph that provide the total cost for specific numbers of downloads. Suppose the graph indicates the following points:
- Point 1: ( (N_1, C_1) = (0, \$10) )
- Point 2: ( (N_2, C_2) = (5, \$20) )
Using these points, we can set up the following equations:
- For Point 1:
[ C_1 = m \times N_1 + b ]
[ 10 = m \times 0 + b ]
[ b = 10 ] - For Point 2:
[ C_2 = m \times N_2 + b ]
[ 20 = m \times 5 + 10 ]
[ 20 = 5m + 10 ]
[ 10 = 5m ]
[ m = 2 ]
Therefore, the monthly subscription fee ( b ) is \$10, and the unit cost per film ( m ) is \$2.
(b) Calculating the Number of Films Watched Based on the Monthly Bill:
If your monthly bill is \$14.50, we can use the cost function to determine the number of films downloaded:
[ C = mN + b ]
Substituting the known values:
[ 14.50 = 2N + 10 ]
[ 4.50 = 2N ]
[ N = \frac{4.50}{2} ]
[ N = 2.25 ]
Since the number of films downloaded must be a whole number, this result suggests that there might be a discrepancy in the provided data or an additional factor affecting the total cost. It’s possible that the graph points or the total bill amount include other charges or discounts not accounted for in this simple linear model.
Explanation:
Linear cost functions are commonly used to represent scenarios where there is a fixed base cost (such as a subscription fee) and a variable cost that depends on usage (like a per-film charge). The general form of such a function is:
[ C(N) = mN + b ]
Where:
- ( C(N) ) is the total cost associated with downloading ( N ) films.
- ( m ) is the marginal cost per film, representing the increase in total cost for each additional film downloaded.
- ( b ) is the fixed cost, corresponding to the monthly subscription fee that is incurred regardless of the number of films downloaded.
In this context, the slope of the cost function (( m )) indicates the rate at which costs increase with each additional film, while the y-intercept (( b )) reflects the base cost when no films are downloaded.
By analyzing specific data points from the cost graph, we can derive these parameters. For instance, if at zero downloads the cost is \$10, this directly reveals the fixed monthly subscription fee. Observing how the total cost changes with additional downloads allows us to calculate the per-film charge.
However, real-world scenarios may introduce complexities not captured by a simple linear model. Factors such as promotional discounts, taxes, or additional fees could affect the total monthly bill, leading to non-integer solutions when calculating usage based solely on the bill amount. In such cases, it’s essential to consider these additional elements to accurately determine usage patterns.
Visual Representation:
A graph illustrating the total monthly cost ( C ) as a function of the number of films downloaded ( N ) would typically display a straight line starting at the fixed cost on the y-axis (when ( N = 0 )) and increasing linearly with a slope equal to the unit cost per film.
For a monthly subscription fee of \$10 and a per-film cost of \$2, the graph would start at ( (0, \$10) ) and rise with a slope of 2.