A stone is dropped from the roof of a high building. A second stone is dropped 1.50 s later. How far apart are the stones when the second one has reached a speed of 12.0 m/s?
The correct answer and explanation is :
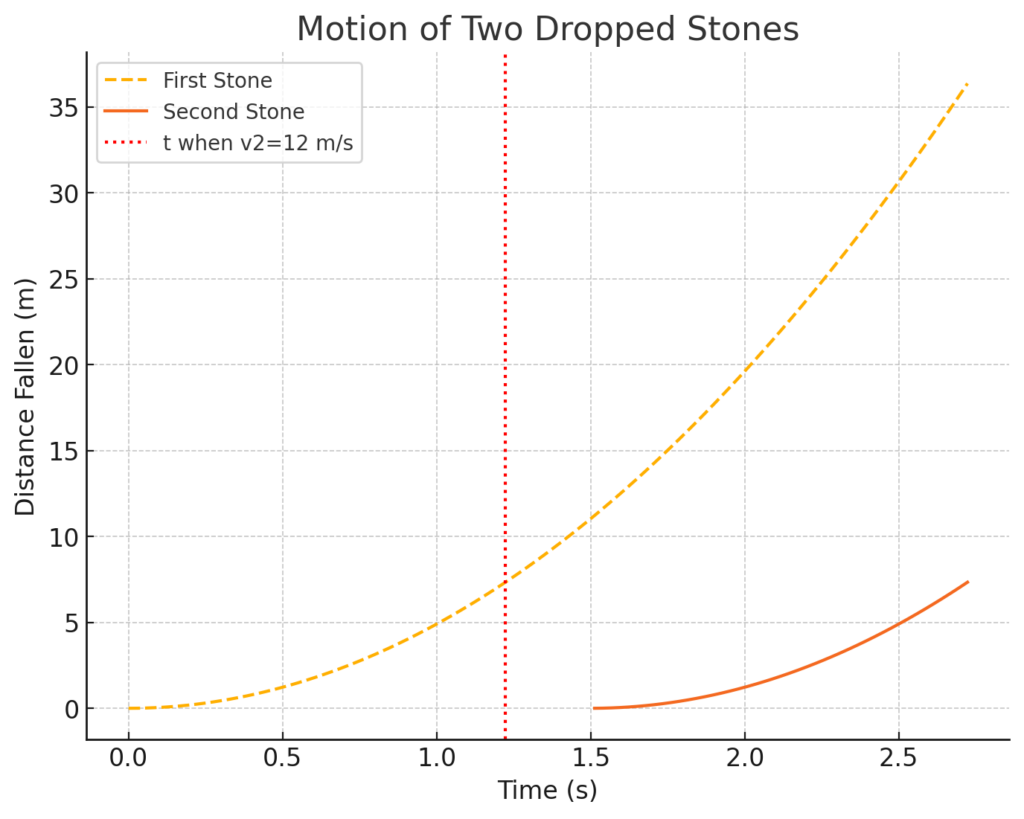
The two stones are 29.04 meters apart when the second stone reaches a speed of 12.0 m/s.
Explanation:
- Understanding the Motion
- Both stones experience free fall, meaning they accelerate downward at 9.81 m/s² due to gravity.
- The first stone is dropped 1.5 seconds earlier than the second stone.
- Finding the Time for the Second Stone
- The velocity of an object in free fall is given by:
[
v = g t
] - Solving for time ( t ) when ( v = 12.0 ) m/s:
[
t = \frac{12.0}{9.81} \approx 1.22 \text{ seconds}
] - So, when the second stone reaches 12.0 m/s, it has been falling for 1.22 seconds.
- Calculating Distance Fallen by Each Stone
- The distance fallen is given by the formula:
[
d = \frac{1}{2} g t^2
] - First stone has fallen for ( 1.22 + 1.5 = 2.72 ) seconds:
[
d_1 = \frac{1}{2} \times 9.81 \times (2.72)^2 = 36.34 \text{ meters}
] - Second stone has fallen for 1.22 seconds:
[
d_2 = \frac{1}{2} \times 9.81 \times (1.22)^2 = 7.30 \text{ meters}
] - The distance between the stones:
[
d_1 – d_2 = 36.34 – 7.30 = 29.04 \text{ meters}
]
Conclusion:
At the moment when the second stone reaches 12.0 m/s, the first stone is already 29.04 meters below it due to its head start of 1.5 seconds.