Convert the following binary numbers into decimal:
(a) 100001
(b) 100111
(c) 101010
(d) 111001
(e) 1100000
(f) 11111101
(g) 11110010
(h) 11111111
The correct answer and explanation is :
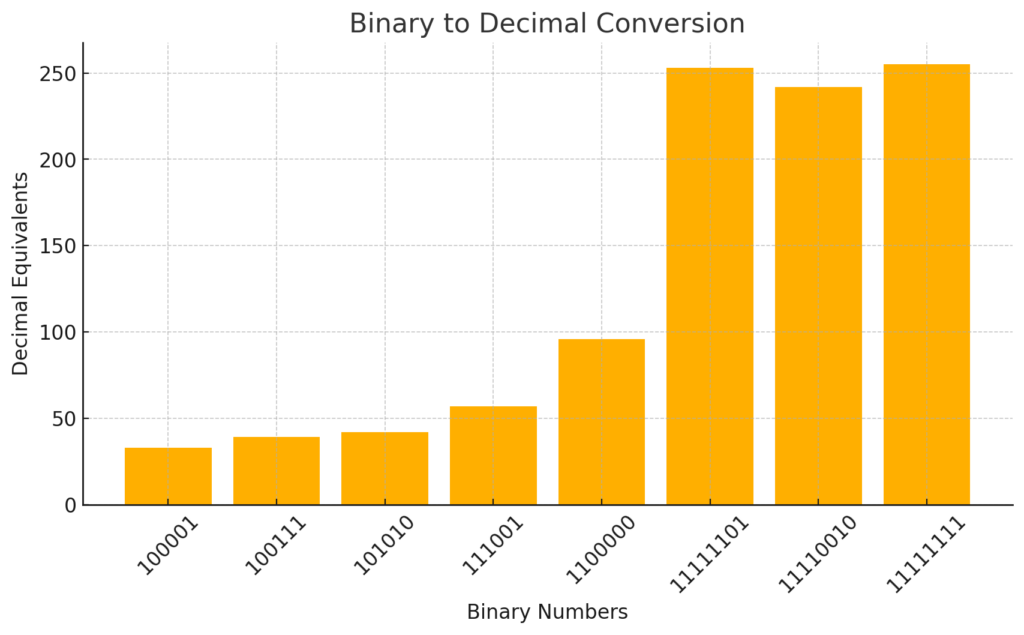
Understanding Binary to Decimal Conversion:
Binary is a base-2 number system, meaning it consists only of the digits 0 and 1. Each position in a binary number represents a power of 2, starting from (2^0) at the rightmost position.
To convert binary to decimal, sum up the values of the positions where there is a 1.
Conversions:
(a) 100001
[
(1 \times 2^5) + (0 \times 2^4) + (0 \times 2^3) + (0 \times 2^2) + (0 \times 2^1) + (1 \times 2^0) = 32 + 1 = 33
]
(b) 100111
[
(1 \times 2^5) + (0 \times 2^4) + (0 \times 2^3) + (1 \times 2^2) + (1 \times 2^1) + (1 \times 2^0) = 32 + 4 + 2 + 1 = 39
]
(c) 101010
[
(1 \times 2^5) + (0 \times 2^4) + (1 \times 2^3) + (0 \times 2^2) + (1 \times 2^1) + (0 \times 2^0) = 32 + 8 + 2 = 42
]
(d) 111001
[
(1 \times 2^5) + (1 \times 2^4) + (1 \times 2^3) + (0 \times 2^2) + (0 \times 2^1) + (1 \times 2^0) = 32 + 16 + 8 + 1 = 57
]
(e) 1100000
[
(1 \times 2^6) + (1 \times 2^5) + (0 \times 2^4) + (0 \times 2^3) + (0 \times 2^2) + (0 \times 2^1) + (0 \times 2^0) = 64 + 32 = 96
]
(f) 11111101
[
(1 \times 2^7) + (1 \times 2^6) + (1 \times 2^5) + (1 \times 2^4) + (1 \times 2^3) + (1 \times 2^2) + (0 \times 2^1) + (1 \times 2^0) = 253
]
(g) 11110010
[
(1 \times 2^7) + (1 \times 2^6) + (1 \times 2^5) + (1 \times 2^4) + (0 \times 2^3) + (0 \times 2^2) + (1 \times 2^1) + (0 \times 2^0) = 242
]
(h) 11111111
[
(1 \times 2^7) + (1 \times 2^6) + (1 \times 2^5) + (1 \times 2^4) + (1 \times 2^3) + (1 \times 2^2) + (1 \times 2^1) + (1 \times 2^0) = 255
]
This method allows for an easy conversion of binary numbers to decimal by summing the powers of 2 where there are 1s.