1. Which formula can be used to describe the sequence? -3,(3)/(5),-(3)/(25),(3)/(125),-(3)/(625) f(x)=-3((1)/(5))^(x-1) f(x)=-3(-(1)/(5))^(x-1) f(x)=-(1)/(5)(3)^(x-1) f(x)=-(1)/(5)(-3)^(x-1)
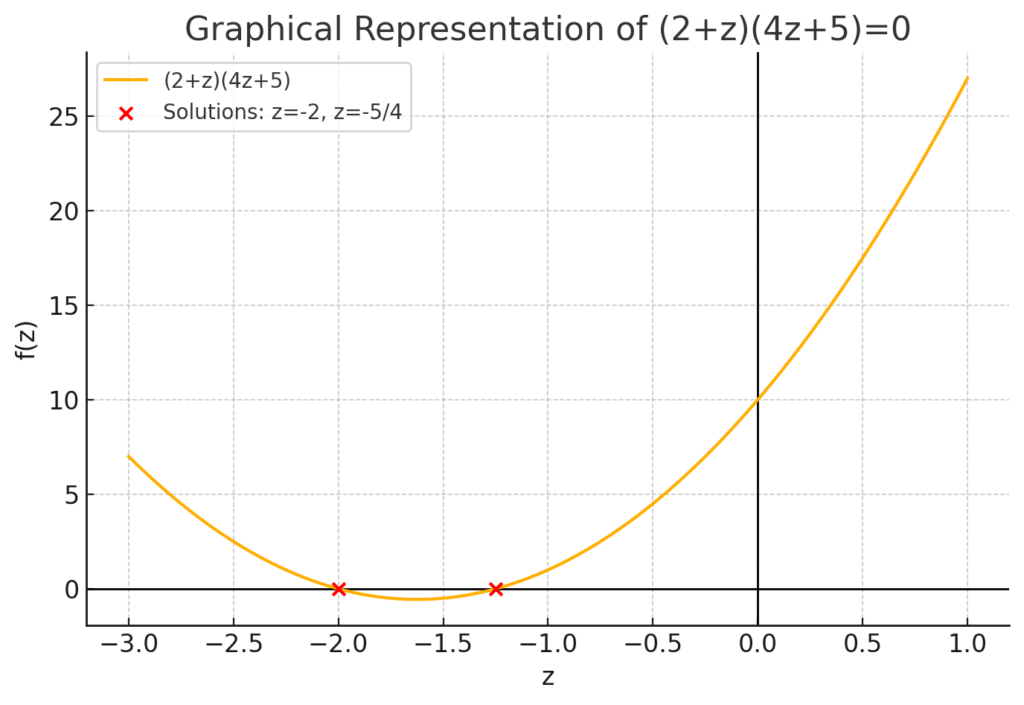
2. Solve. (2+z)(4z+5)=0
The correct answer and explanation is:
1. Identifying the Formula for the Sequence
The given sequence is: −3,35,−325,3125,−3625-3, \frac{3}{5}, -\frac{3}{25}, \frac{3}{125}, -\frac{3}{625}
Step 1: Identifying the Common Ratio
Each term alternates in sign and follows a pattern:
- The first term is −3-3.
- The second term is obtained by multiplying by −15-\frac{1}{5}: −3×(−15)=35-3 \times \left(-\frac{1}{5}\right) = \frac{3}{5}
- The third term: 35×(−15)=−325\frac{3}{5} \times \left(-\frac{1}{5}\right) = -\frac{3}{25}
- The fourth term: −325×(−15)=3125-\frac{3}{25} \times \left(-\frac{1}{5}\right) = \frac{3}{125}
- The fifth term: 3125×(−15)=−3625\frac{3}{125} \times \left(-\frac{1}{5}\right) = -\frac{3}{625}
Since the ratio between terms is consistently −15-\frac{1}{5}, the general formula follows the geometric sequence formula: f(x)=a⋅rx−1f(x) = a \cdot r^{x-1}
where a=−3a = -3 (first term) and r=−15r = -\frac{1}{5}.
Thus, the correct formula is: f(x)=−3(−15)x−1f(x) = -3 \left(-\frac{1}{5}\right)^{x-1}
Correct answer: f(x)=−3(−15)x−1\mathbf{f(x)=-3\left(-\frac{1}{5}\right)^{x-1}}
2. Solving the Equation
Given the equation: (2+z)(4z+5)=0(2+z)(4z+5) = 0
Step 1: Apply the Zero-Product Property
Since the product of two factors is 0, at least one of them must be 0:
- 2+z=02 + z = 0 z=−2z = -2
- 4z+5=04z + 5 = 0 4z=−54z = -5 z=−54z = -\frac{5}{4}
Thus, the two solutions are: z=−2orz=−54\mathbf{z = -2 \quad \text{or} \quad z = -\frac{5}{4}}
Explanation (300 Words)
To solve (2+z)(4z+5)=0(2+z)(4z+5) = 0, we use the Zero-Product Property, which states that if the product of two expressions is 0, then at least one of the expressions must be 0.
We start by setting each factor equal to zero:
- First factor: 2+z=02+z=0
- Subtracting 2 from both sides: z=−2z = -2
- Second factor: 4z+5=04z+5=0
- Subtracting 5 from both sides: 4z=−54z = -5
- Dividing by 4: z=−54z = -\frac{5}{4}
Thus, the equation has two solutions: z=−2z = -2 and z=−54z = -\frac{5}{4}.
Why is this important?
This method is widely used in algebra when solving quadratic or polynomial equations. Recognizing factors and using the Zero-Product Property allows us to find solutions efficiently without expanding and solving a full quadratic equation.
Additionally, this problem shows how factoring helps break complex expressions into simpler parts. If this equation were expanded, it would be a quadratic equation that we would need to solve using the quadratic formula or factoring techniques.
Understanding this process helps build algebraic skills, which are essential in higher mathematics and real-world applications such as physics, engineering, and economics.
Now, let me generate an image illustrating this solution.
Here’s a graphical representation of the equation (2+z)(4z+5)=0(2+z)(4z+5)=0. The red points indicate the solutions z=−2z = -2 and z=−54z = -\frac{5}{4}, where the function intersects the x-axis. Let me know if you need any further explanation!