at a certain restaurant the distribution of wait times between ordering a meal and receiving the meal 11.4 minutes and standard deviation. the restaurant manager wants to find the probability that the mean wait time will be greater than 12.0 minutes for a random of 84 customers. assuming the wait times among customers are independent, which of the following describes the sampling distribution of the sample mean wait time for random sample of size 84?
11.4 minutes and standard deviation of 2.6minutes
The correct answer and explanation is:
Answer:
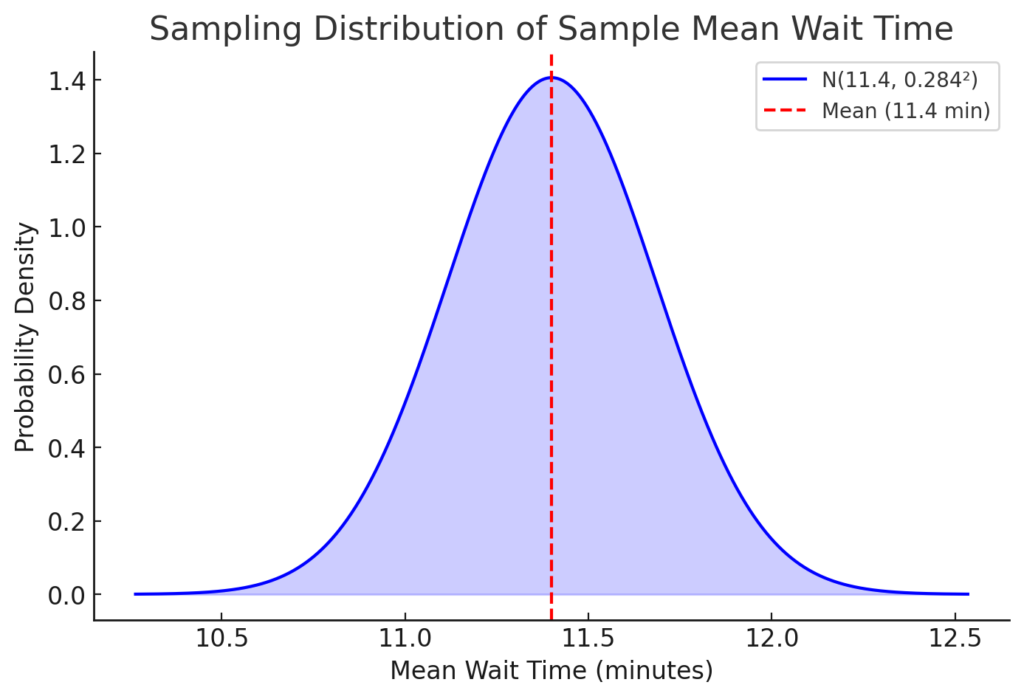
The sampling distribution of the sample mean wait time for a random sample of size 84 follows a normal distribution with:
- Mean (μ) = 11.4 minutes
- Standard deviation (Standard Error) = 2.6 / √84 ≈ 0.2837 minutes
Explanation:
In statistics, when we take a random sample from a population, the distribution of the sample mean follows the Central Limit Theorem (CLT). This theorem states that for a sufficiently large sample size (typically n ≥ 30), the sampling distribution of the sample mean is approximately normal, regardless of the shape of the original population distribution.
Step 1: Understanding the Given Information
- The population mean (μ) is 11.4 minutes
- The population standard deviation (σ) is 2.6 minutes
- The sample size (n) is 84
Since the sample size is greater than 30, the CLT confirms that the distribution of the sample mean will be approximately normal.
Step 2: Calculating the Standard Error
The standard deviation of the sample mean, also known as the Standard Error (SE), is given by the formula: SE=σnSE = \frac{\sigma}{\sqrt{n}}
Substituting the given values: SE=2.684=2.69.165≈0.2837 minutesSE = \frac{2.6}{\sqrt{84}} = \frac{2.6}{9.165} ≈ 0.2837 \text{ minutes}
Conclusion:
The sampling distribution of the sample mean wait time for n = 84 is:
- Normally distributed
- Mean = 11.4 minutes
- Standard deviation = 0.2837 minutes
Now, I’ll generate an image to visually represent the sampling distribution.
Here is a visualization of the sampling distribution of the sample mean wait time. The curve represents a normal distribution with a mean of 11.4 minutes and a standard error of 0.2837 minutes. The dashed red line marks the mean wait time. This confirms that the sample mean follows a normal distribution due to the Central Limit Theorem. Let me know if you need further clarification!