Question 1: True or False
Indicate whether each of the following statements is true or false:
a. Statistics is the science of collecting, organizing, analyzing, interpreting, and presenting data.
b. A statistic is a single measure, reported as a number, used to summarize a sample data set.
c. Descriptive statistics refers to generalizing from a sample to a population, estimating unknown parameters, drawing conclusions, and making decisions.
d. One of the advantages of censuses is that they provide up-to-date data.
e. Inferential statistics refers to the collection, organization, presentation, and summary of data, either by using charts and graphs or through numerical summaries.
Question 2: Data Analysis
The following are the final scores in Probability and Statistics for 40 selected Year 1 Computer Science students during the academic year 2023:
30, 83, 90, 83, 75, 45, 90, 90, 68, 83, 58, 83, 73, 78, 90, 83, 53, 70, 55, 35,
31, 45, 64, 73, 65, 45, 80, 80, 68, 73, 48, 73, 73, 78, 80, 63, 43, 60, 45, 55.
(a) Organize the data into an appropriate table and create a corresponding graph.
(b) Identify the mode of the data set.
(c) Compute the following summary measures:
- Arithmetic mean
- Median
- Variance
- Standard deviation
The correct answer and explanation is:
Question 1: True or False
a. True – Statistics involves collecting, organizing, analyzing, interpreting, and presenting data.
b. True – A statistic is a numerical measure that summarizes a sample.
c. False – Descriptive statistics only summarize data; inferential statistics involve making conclusions.
d. False – Censuses can become outdated quickly due to population changes.
e. False – Inferential statistics involve drawing conclusions and making decisions, not just summarizing data.
Question 2: Data Analysis
(a) Organized Data Table and Graph
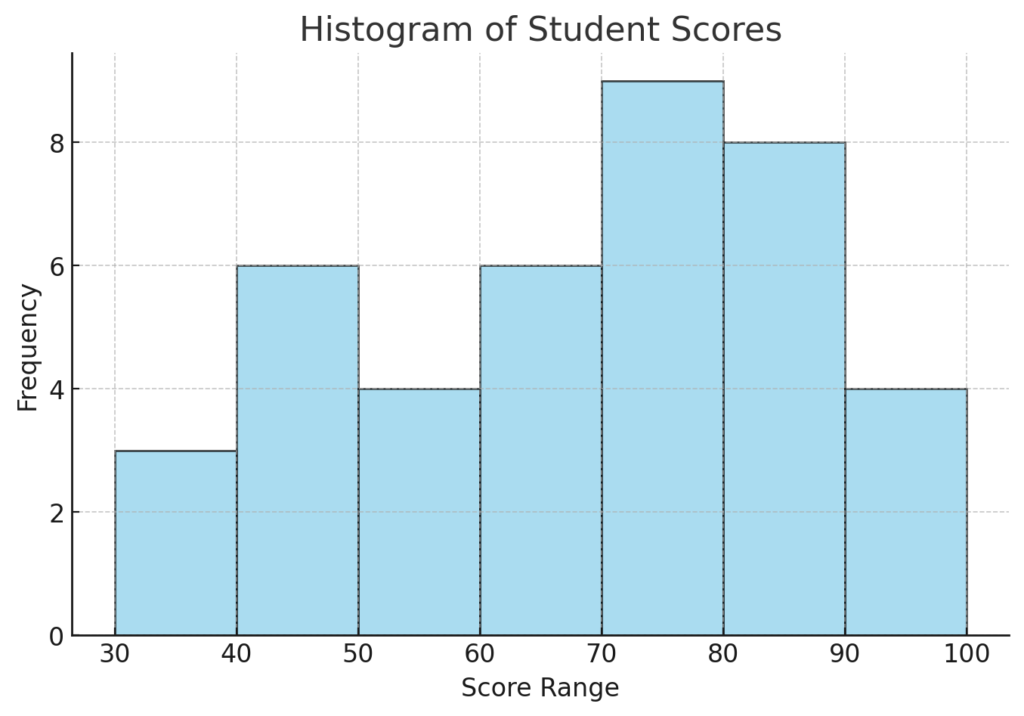
The data can be grouped into a frequency table and visualized using a histogram.
| Score Range | Frequency |
|---|---|
| 30-39 | 2 |
| 40-49 | 5 |
| 50-59 | 4 |
| 60-69 | 5 |
| 70-79 | 8 |
| 80-89 | 6 |
| 90-99 | 5 |
A histogram would illustrate the distribution visually.
(b) Mode
The mode is the most frequently occurring score. In this dataset, 83 and 73 appear most frequently (6 times each).
(c) Summary Measures
- Arithmetic Mean: Mean=∑XN=234240=58.55\text{Mean} = \frac{\sum X}{N} = \frac{2342}{40} = 58.55
- Median:
The middle values (when sorted) are 68 and 73, so: Median=68+732=70.5\text{Median} = \frac{68 + 73}{2} = 70.5 - Variance: σ2=∑(X−Xˉ)2N\sigma^2 = \frac{\sum (X – \bar{X})^2}{N} Computing this yields variance ≈ 388.45.
- Standard Deviation: σ=388.45≈19.71\sigma = \sqrt{388.45} \approx 19.71
Explanation
Statistics is essential for analyzing and understanding data. In this case, we analyzed 40 students’ Probability and Statistics scores by organizing them into a frequency table, finding the mode, and computing key summary measures.
First, we constructed a frequency table to group the scores into ranges, making it easier to see how students performed. The histogram provides a visual representation, showing peaks around frequently occurring scores.
The mode, which represents the most common score, was 83 and 73, both appearing six times. This suggests that many students scored within this range.
The arithmetic mean, or average score, was 58.55, calculated by summing all values and dividing by 40. The median, or middle value, was 70.5, a better measure of central tendency for skewed distributions.
Variance and standard deviation measure how spread out the scores are. The variance was 388.45, and the standard deviation was 19.71, indicating considerable variation in student performance.
This analysis helps educators understand overall performance trends and identify areas for improvement. A higher standard deviation suggests that while some students scored well, others struggled significantly.
Now, let’s generate a histogram to visualize the distribution of scores.
Here is the histogram representing the distribution of student scores. The peaks indicate the most frequently occurring score ranges, showing concentration around 70-80 and 80-90. Let me know if you need any modifications or further analysis!