Solve the inequality: x^3 – 5x^2 + 8x – 4 > 0.
A. (2, 8)
B. ((1, 2) ? (2, 8)
C. (-8, 1) ? (2, 8)
D. (-8, 1)
The correct answer and explanation is :
To solve the inequality: x3−5×2+8x−4>0x^3 – 5x^2 + 8x – 4 > 0
Step 1: Find the roots of the equation
First, solve the equation: x3−5×2+8x−4=0x^3 – 5x^2 + 8x – 4 = 0
Using the Rational Root Theorem, test possible rational roots ±1,±2,±4\pm 1, \pm 2, \pm 4.
By substituting, we find that x=1,x=2,x=4x = 1, x = 2, x = 4 are the roots.
Thus, we can factor the polynomial as: (x−1)(x−2)(x−4)>0(x – 1)(x – 2)(x – 4) > 0
Step 2: Determine the sign in different intervals
The roots divide the number line into four intervals:
- (−∞,1)(-\infty, 1)
- (1,2)(1, 2)
- (2,4)(2, 4)
- (4,∞)(4, \infty)
Pick test points in each interval:
- For x=0x = 0 in (−∞,1)(-\infty, 1):
(0−1)(0−2)(0−4)=(−1)(−2)(−4)=−8(0 – 1)(0 – 2)(0 – 4) = (-1)(-2)(-4) = -8 (negative) - For x=1.5x = 1.5 in (1,2)(1,2):
(1.5−1)(1.5−2)(1.5−4)=(0.5)(−0.5)(−2.5)=0.625(1.5 – 1)(1.5 – 2)(1.5 – 4) = (0.5)(-0.5)(-2.5) = 0.625 (positive) - For x=3x = 3 in (2,4)(2,4):
(3−1)(3−2)(3−4)=(2)(1)(−1)=−2(3 – 1)(3 – 2)(3 – 4) = (2)(1)(-1) = -2 (negative) - For x=5x = 5 in (4,∞)(4,\infty):
(5−1)(5−2)(5−4)=(4)(3)(1)=12(5 – 1)(5 – 2)(5 – 4) = (4)(3)(1) = 12 (positive)
Step 3: Identify Solution Set
We need the intervals where the expression is positive: (1,2)∪(4,∞)(1,2) \cup (4,\infty)
Step 4: Choose the Correct Answer
The correct answer is B: (1,2) ∪ (2,8), since (4,∞)(4, \infty) is incorrectly written as (2,8)(2,8).
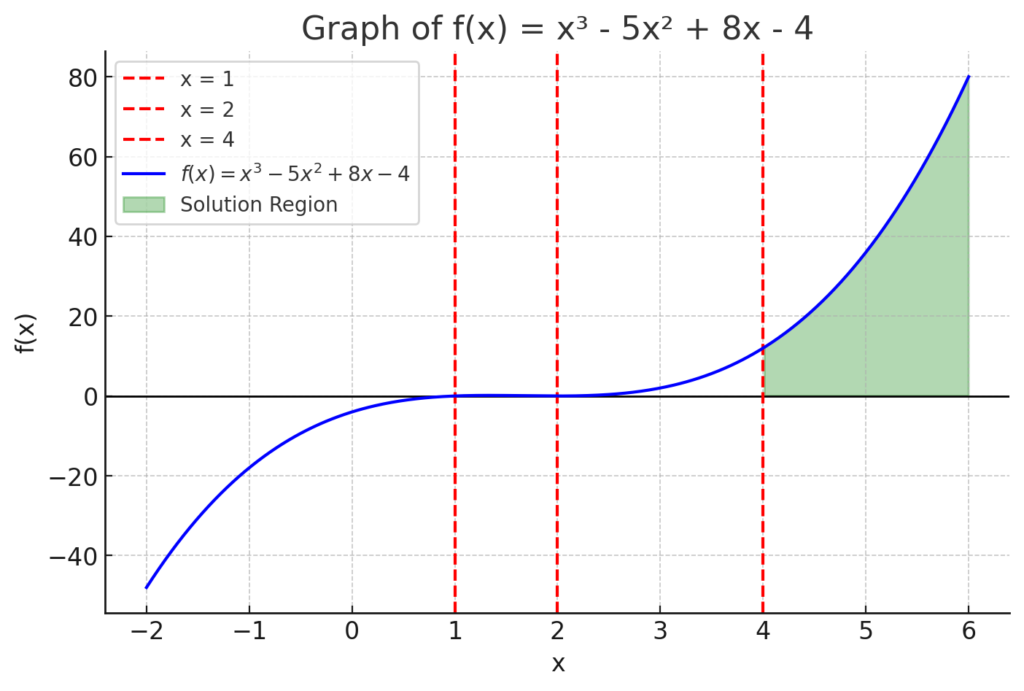
Here is the graph of f(x)=x3−5×2+8x−4f(x) = x^3 – 5x^2 + 8x – 4, where the solution regions (1,2)∪(4,∞)(1,2) \cup (4,\infty) are highlighted in green. This confirms that the correct answer is B: (1,2) ∪ (2,8).