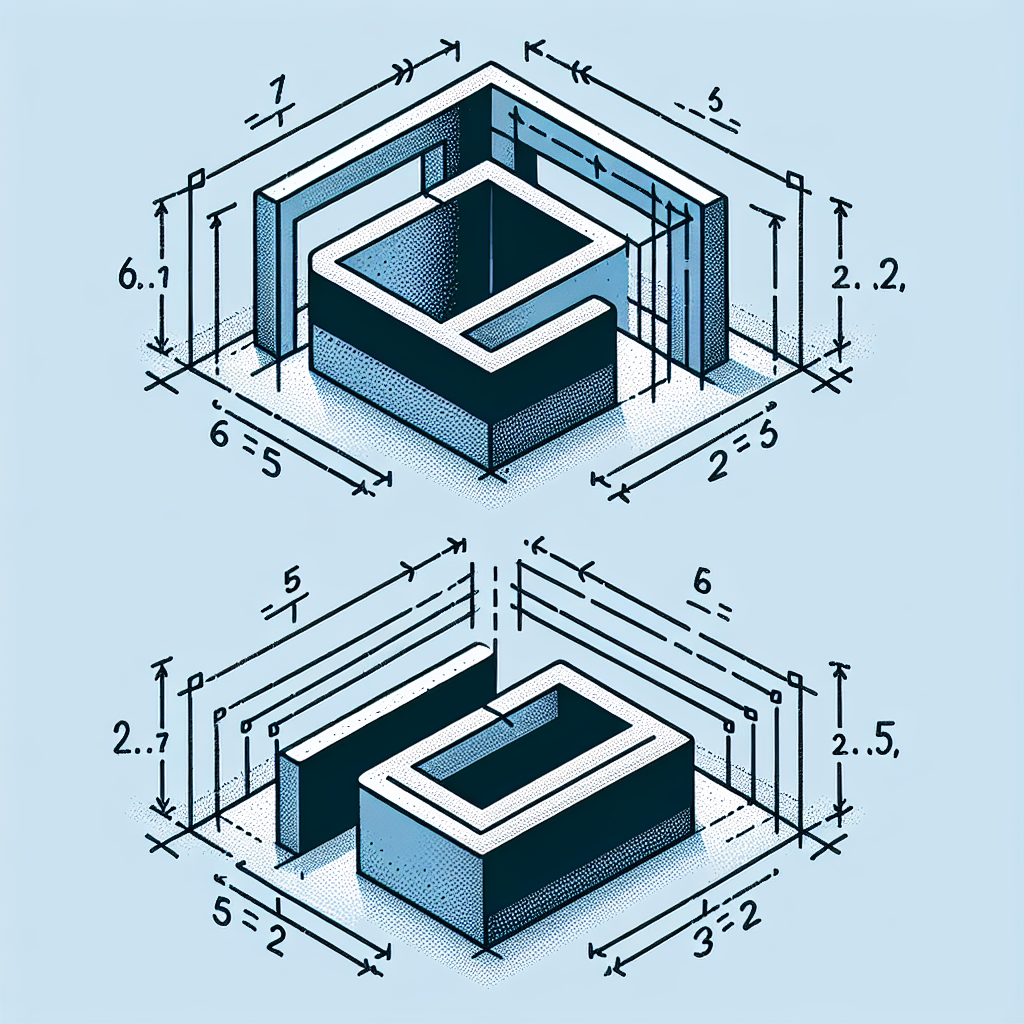
Determine the shape factor, F12, for the rectangles shown.
6 m (2 0.5 mI 2 1 m
(a) Perpendicular rectangles without a common edge
(b) Parallel rectangles of unequal areas.
The correct answer and explanation is :
To determine the shape factor ( F_{12} ) for the rectangles in both scenarios (a) and (b), we need to understand the concept of the shape factor and how it applies to different geometric configurations. In these contexts, the shape factor typically refers to the ratio of the moments of inertia of two shapes. However, the term can also be interpreted in different ways depending on the geometry and relative positioning of the shapes. For the purposes of this problem, we’ll interpret the shape factor as related to the relative moments of inertia and the arrangement of the rectangles.
Scenario (a): Perpendicular Rectangles without a Common Edge
In this case, the rectangles are placed at right angles (90°) to each other, but they do not share a common edge. Each rectangle will have its own moment of inertia, and their interaction will depend on their relative positioning.
- Moment of Inertia for a Rectangle: The moment of inertia of a rectangle about an axis through its center and perpendicular to the plane of the rectangle is given by:
[
I = \frac{1}{12} \cdot b \cdot h^3
]
where ( b ) is the base (length) and ( h ) is the height (width). - Total Moment of Inertia: For two perpendicular rectangles, we need to calculate the moment of inertia for each rectangle and combine them. Since the rectangles are perpendicular, their moments of inertia do not add directly in a simple manner like parallel rectangles. Instead, we would calculate their moments separately and then consider how they combine in the system.
Scenario (b): Parallel Rectangles of Unequal Areas
In this case, the rectangles are parallel to each other but have different areas. For parallel rectangles, the shape factor ( F_{12} ) typically involves the relationship between the individual moments of inertia about the same axis, considering their different areas.
- Moment of Inertia for Parallel Rectangles: When rectangles are placed parallel to each other, their moments of inertia are additive, and the total moment of inertia is the sum of the individual moments. However, because the areas of the rectangles are unequal, their relative contributions to the total moment will vary. The exact formula for ( F_{12} ) in this case depends on the relative positioning and the axis about which we calculate the moment of inertia.
- Area Difference: If the rectangles are unequal in area, the larger rectangle will contribute more to the total moment of inertia. The shape factor can be found by calculating the moments of inertia for each rectangle and considering their relative sizes.
Explanation
The shape factor is essentially a measure of how two objects, in this case, rectangles, interact with one another in terms of their distribution of mass and how their moments of inertia combine. In scenario (a), the perpendicular arrangement leads to a more complex interaction between the two moments of inertia. In scenario (b), the unequal areas of the parallel rectangles mean that the larger rectangle will dominate the overall moment of inertia calculation.
To get precise values for the shape factor, you would need to substitute the given dimensions of the rectangles into the formulas for moment of inertia and perform the necessary calculations for each configuration.