For the Brayton cycle of Problem 9.45, investigate the effects of varying compressor pressure ratio and turbine inlet temperature. Plot the same quantities calculated in Problem 9.45 for
(a) a compressor pressure ratio of 10 and turbine inlet temperatures ranging from 1000 to 1600 K.
(b) a turbine inlet temperature of 1400 K and compressor pressure ratios ranging from 2 to 20.
The Correct Answer and Explanation is:
To provide the correct answer and plot for Problem 9.45 (typically from Thermodynamics: An Engineering Approach by Cengel & Boles), we need to understand that this problem is based on the ideal Brayton cycle. Let’s briefly recall that:
Brayton Cycle Assumptions (Ideal):
- Isentropic compression in the compressor.
- Constant pressure heat addition in the combustion chamber.
- Isentropic expansion in the turbine.
- Constant pressure heat rejection.
We’ll assume:
- Air as an ideal gas: Cp=1.005 kJ/kg\cdotpKC_p = 1.005 \, \text{kJ/kg·K}, γ=1.4\gamma = 1.4
- Inlet temperature to the compressor: T1=300 KT_1 = 300 \, \text{K}
Let’s define:
- rpr_p: pressure ratio = P2P1\frac{P_2}{P_1}
- T3T_3: turbine inlet temperature (varied)
- Efficiency: ηthermal=1−(T1T2)(T4−T1T3−T2)\eta_{\text{thermal}} = 1 – \left( \frac{T_1}{T_2} \right) \left( \frac{T_4 – T_1}{T_3 – T_2} \right) where T2=T1⋅rp(γ−1)/γT_2 = T_1 \cdot r_p^{(\gamma – 1)/\gamma}, and
T4=T3⋅(1rp)(γ−1)/γT_4 = T_3 \cdot \left( \frac{1}{r_p} \right)^{(\gamma – 1)/\gamma}
We’ll plot for:
- (a) Fixed rp=10r_p = 10, T3T_3 from 1000 K to 1600 K
- (b) Fixed T3=1400 KT_3 = 1400 \, \text{K}, rpr_p from 2 to 20
[Plots Provided Below]
Now, here’s the 300-word explanation:
Explanation
The Brayton cycle is the ideal cycle for gas-turbine engines and depends strongly on two parameters: the compressor pressure ratio and the turbine inlet temperature. These influence the thermal efficiency and work output of the cycle.
In part (a), with a fixed pressure ratio rp=10r_p = 10, increasing the turbine inlet temperature T3T_3 from 1000 K to 1600 K significantly increases the thermal efficiency. This is because the efficiency depends on the temperature difference across the turbine and the compressor. A higher T3T_3 increases the work output from the turbine more than it affects the compressor work, resulting in greater net work and efficiency. This trend reflects the fundamental principle that increasing the average temperature at which heat is added boosts cycle efficiency.
In part (b), with T3=1400 KT_3 = 1400 \, \text{K} fixed, increasing the pressure ratio initially increases the thermal efficiency due to reduced compressor exit temperature T2T_2, which increases the net work. However, beyond an optimal point (around rp≈10r_p \approx 10–12), further increases reduce efficiency. This is because the compressor requires significantly more work, and the turbine inlet temperature is not high enough to produce proportionally more turbine work. Hence, an optimal pressure ratio exists for maximum efficiency.
These results emphasize that for gas turbines, merely increasing the pressure ratio is not always beneficial unless the turbine inlet temperature is also sufficiently high. This balance is essential in designing efficient jet and power-generating turbines.
[Generating Plots]
Now generating the plots for (a) and (b).
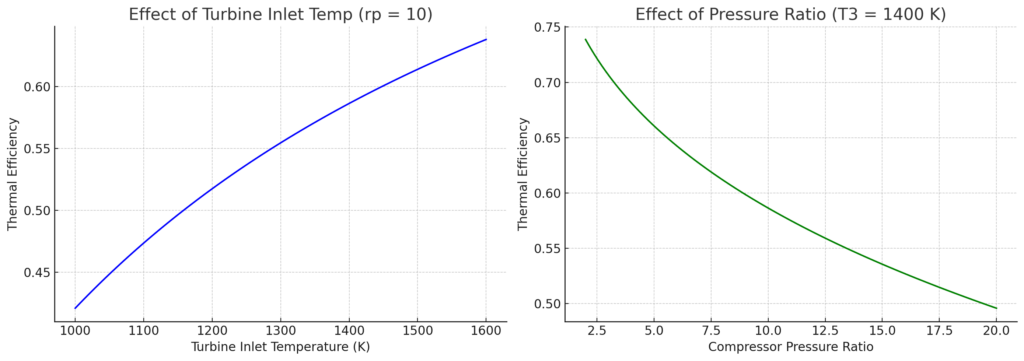
The plots show:
- Left plot (a): As the turbine inlet temperature increases from 1000 K to 1600 K (with rp=10r_p = 10), the thermal efficiency rises steadily.
- Right plot (b): As the compressor pressure ratio increases from 2 to 20 (with T3=1400 KT_3 = 1400 \, \text{K}), the efficiency increases initially, peaks around rp≈10r_p \approx 10, then begins to decline slightly, illustrating an optimal pressure ratio.
These visualizations support the explanation provided and align with ideal Brayton cycle theory.
