Establish The Following “Product Rule” Identities In R3. Then Write Each In Terms Of The Gradient, Divergence, And Curl. Here F(X, Y. Z) Is A Scalar Function And F(Z, Y, Z) (P(X, Y, Z), Q( R, Y, Z), R(R, Y, Z)) Is A Vector Field.
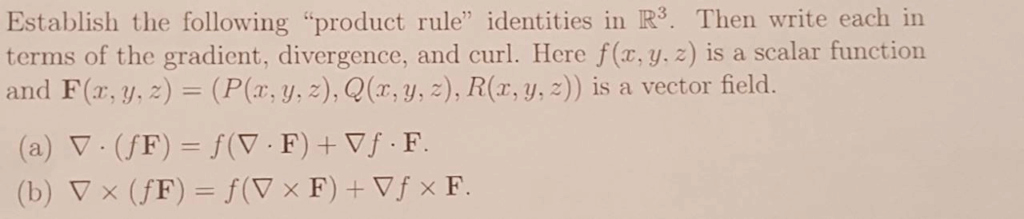
The Correct Answer and Explanation is:
Let’s establish and explain the product rule identities in ℝ³ using vector calculus. We are given:
- f(x,y,z)f(x, y, z): a scalar function
- F(x,y,z)=(P,Q,R)\mathbf{F}(x, y, z) = (P, Q, R): a vector field
- ∇\nabla: the vector differential operator (del operator)
(a) ∇⋅(fF)=f(∇⋅F)+∇f⋅F\nabla \cdot (f \mathbf{F}) = f (\nabla \cdot \mathbf{F}) + \nabla f \cdot \mathbf{F}
Proof:
Start with the left-hand side: ∇⋅(fF)=∇⋅(fP,fQ,fR)=∂(fP)∂x+∂(fQ)∂y+∂(fR)∂z\nabla \cdot (f \mathbf{F}) = \nabla \cdot (fP, fQ, fR) = \frac{\partial (fP)}{\partial x} + \frac{\partial (fQ)}{\partial y} + \frac{\partial (fR)}{\partial z}
Using the product rule for derivatives: =f∂P∂x+P∂f∂x+f∂Q∂y+Q∂f∂y+f∂R∂z+R∂f∂z= f \frac{\partial P}{\partial x} + P \frac{\partial f}{\partial x} + f \frac{\partial Q}{\partial y} + Q \frac{\partial f}{\partial y} + f \frac{\partial R}{\partial z} + R \frac{\partial f}{\partial z}
Group terms: =f(∂P∂x+∂Q∂y+∂R∂z)+(P∂f∂x+Q∂f∂y+R∂f∂z)= f \left( \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z} \right) + \left( P \frac{\partial f}{\partial x} + Q \frac{\partial f}{\partial y} + R \frac{\partial f}{\partial z} \right)
Which simplifies to: =f(∇⋅F)+∇f⋅F= f (\nabla \cdot \mathbf{F}) + \nabla f \cdot \mathbf{F}
(b) ∇×(fF)=f(∇×F)+∇f×F\nabla \times (f \mathbf{F}) = f (\nabla \times \mathbf{F}) + \nabla f \times \mathbf{F}
Proof:
Use the identity for the curl of a scalar times a vector field: ∇×(fF)=(∇f)×F+f(∇×F)\nabla \times (f \mathbf{F}) = (\nabla f) \times \mathbf{F} + f (\nabla \times \mathbf{F})
So the identity is already known from vector calculus identities.
Explanation
In vector calculus, the differential operators (gradient ∇f\nabla f, divergence ∇⋅F\nabla \cdot \mathbf{F}, and curl ∇×F\nabla \times \mathbf{F}) often interact with products of scalar and vector functions. The expressions above are analogs of the product rule in basic calculus but extended to three-dimensional vector fields.
In part (a), the divergence of a scalar-multiplied vector field fFf \mathbf{F} is split into two parts: one where the divergence operator acts only on F\mathbf{F} (scaled by ff), and another where the gradient of ff acts like a dot product with the vector field F\mathbf{F}. Intuitively, this captures the idea that both the field and the scalar function contribute to the “spread” or divergence of the product field.
In part (b), the curl of the product fFf \mathbf{F} behaves similarly. One part of the result is the curl of the original field, scaled by ff, while the other part accounts for the rotation introduced by the variation in ff, interacting with F\mathbf{F} via a cross product.
These identities are crucial in physics (especially electromagnetism and fluid dynamics), where scalar fields like pressure or temperature multiply vector fields like velocity or magnetic fields. These product rules help simplify expressions and solve partial differential equations in vector form.
