The particle enters this region horizontally from the left and then curves upward, indicating the influence of the magnetic field on its motion.
The Correct Answer and Explanation is:
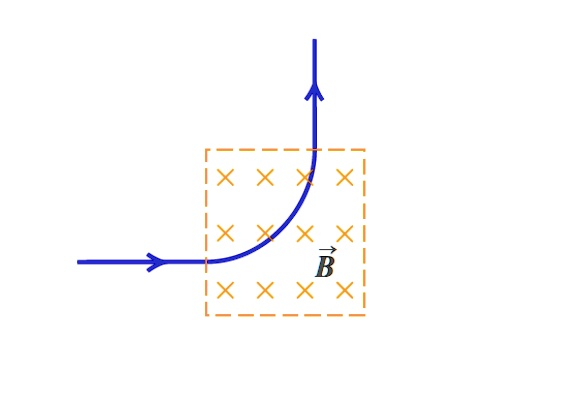
The image shows a charged particle moving through a region with a uniform magnetic field directed into the page (denoted by the orange crosses). The particle enters this region horizontally from the left and then curves upward, indicating the influence of the magnetic field on its motion.
Correct Answer:
The particle is positively charged.
Explanation
This scenario is a classic application of the Lorentz force, which governs the motion of charged particles in magnetic fields. The force F⃗\vec{F} acting on a charged particle of charge qq moving with velocity v⃗\vec{v} in a magnetic field B⃗\vec{B} is given by: F⃗=qv⃗×B⃗\vec{F} = q\vec{v} \times \vec{B}
Given:
- The velocity v⃗\vec{v} of the particle is initially to the right (positive x-direction).
- The magnetic field B⃗\vec{B} is into the page (denoted by the “×” symbols).
- The path of the particle curves upward (toward the positive y-direction).
Let’s apply the right-hand rule for the cross product v⃗×B⃗\vec{v} \times \vec{B}:
- Point your right-hand fingers in the direction of v⃗\vec{v} (to the right).
- Curl your fingers into the page (direction of B⃗\vec{B}).
- Your thumb points upward — the direction of the magnetic force F⃗\vec{F}.
Since the magnetic force is upward, and the force is qv⃗×B⃗q\vec{v} \times \vec{B}, this indicates the charge qq must be positive for the direction of force to match the observed upward curvature.
If the charge were negative, the force direction would be opposite — i.e., downward, which contradicts the observed upward deflection.
Conclusion:
The particle curves upward due to the Lorentz force acting in that direction, which happens only if the particle has a positive charge. This is a direct application of the right-hand rule for positive charges in magnetic fields.
