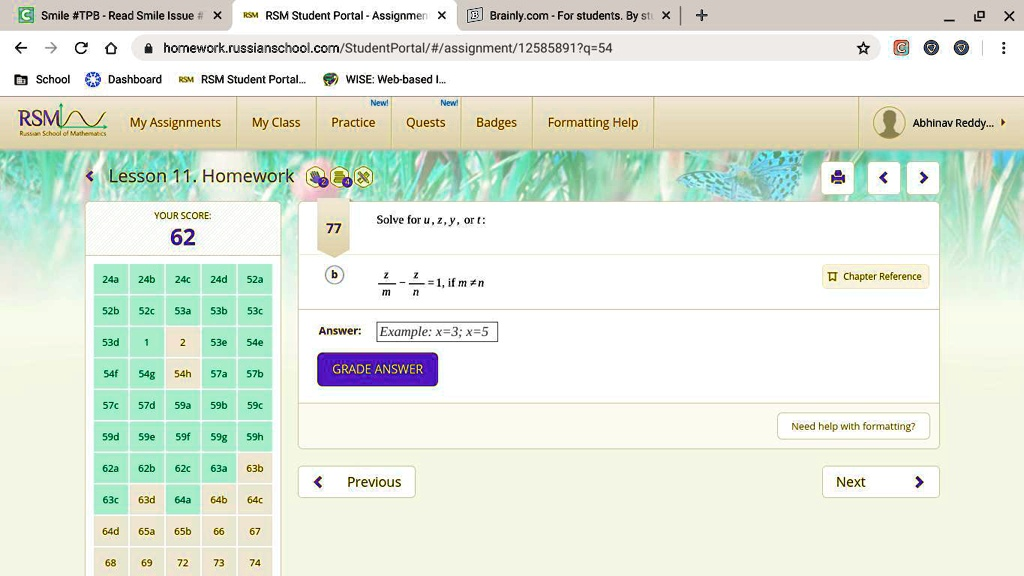
Solve for u, z, y, or t: \frac{z}{m} – \frac{z}{n} = 1, if m \neq n
The Correct Answer and Explanation is:
We are given the equation: zm−zn=1,where m≠n\frac{z}{m} – \frac{z}{n} = 1, \quad \text{where } m \ne n
Step-by-step Solution:
Factor out zz on the left-hand side: z(1m−1n)=1z\left(\frac{1}{m} – \frac{1}{n}\right) = 1
Find a common denominator and simplify: 1m−1n=n−mmn\frac{1}{m} – \frac{1}{n} = \frac{n – m}{mn}
Substitute back into the equation: z⋅n−mmn=1z \cdot \frac{n – m}{mn} = 1
Now solve for zz by multiplying both sides by the reciprocal: z=mnn−mz = \frac{mn}{n – m}
✅ Final Answer:
z=mnn−m\boxed{z = \frac{mn}{n – m}}
Explanation
This equation involves two fractions with the same variable zz, but different denominators mm and nn. The key to solving it efficiently is recognizing that zz is common in both terms and can be factored out.
When we factor out zz from the expression zm−zn\frac{z}{m} – \frac{z}{n}, we treat it like factoring a variable from a polynomial. This leaves us with z(1m−1n)z\left(\frac{1}{m} – \frac{1}{n}\right), which simplifies the left-hand side and allows us to isolate zz.
To simplify the parentheses (1m−1n)\left(\frac{1}{m} – \frac{1}{n}\right), we use a common denominator. The least common denominator of mm and nn is mnmn, and using it gives us the difference of the two fractions as n−mmn\frac{n – m}{mn}.
Now, our equation becomes z⋅n−mmn=1z \cdot \frac{n – m}{mn} = 1. To isolate zz, we divide both sides of the equation by n−mmn\frac{n – m}{mn}, which is the same as multiplying both sides by its reciprocal mnn−m\frac{mn}{n – m}.
This leads to the final result: z=mnn−mz = \frac{mn}{n – m}, provided m≠nm \ne n, which is given in the problem. This ensures that the denominator does not become zero, keeping the solution valid.
This type of algebraic manipulation is common in solving rational equations and emphasizes the importance of factoring and understanding operations with fractions.
