What is the product?\n
\n
\n
\n
\n
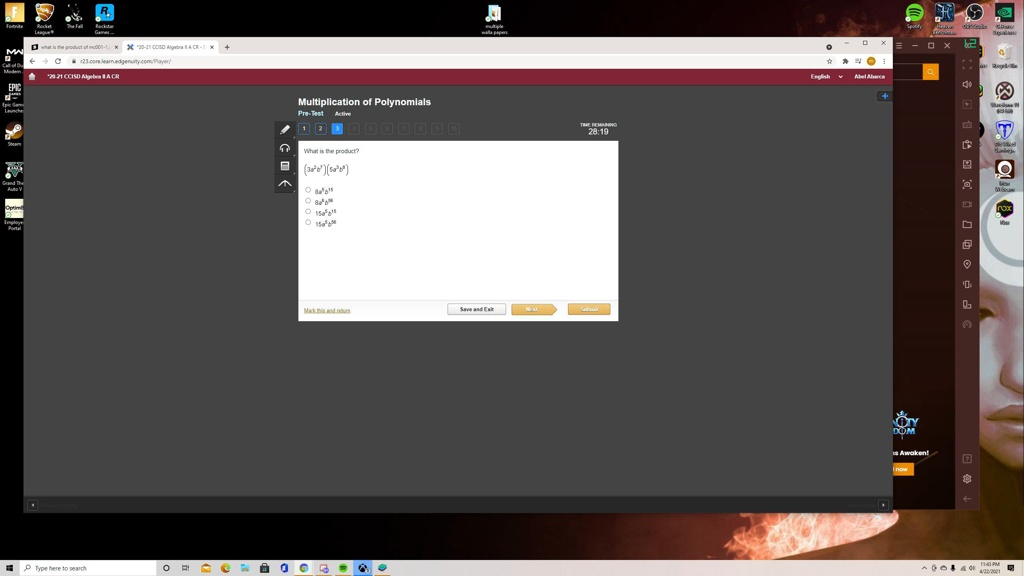
The Correct Answer and Explanation is:
To solve the problem shown in the image, we need to find the product: (3a2b3)(5a3b2)(3a^2b^3)(5a^3b^2)
Step-by-Step Solution:
We are multiplying two monomials: (3a2b3)×(5a3b2)(3a^2b^3) \times (5a^3b^2)
- Multiply the constants (numerical coefficients):
3×5=153 \times 5 = 15
- Multiply the powers of aa:
a2×a3=a2+3=a5a^2 \times a^3 = a^{2+3} = a^5
- Multiply the powers of bb:
b3×b2=b3+2=b5b^3 \times b^2 = b^{3+2} = b^5
Final Answer:
15a5b515a^5b^5
Explanation
When multiplying polynomials or monomials, you apply the product of powers property, which states that if you are multiplying like bases, you add their exponents. This principle is key in simplifying expressions involving variables with exponents.
In the given expression (3a2b3)(5a3b2)(3a^2b^3)(5a^3b^2), we start by addressing each part of the expression systematically.
First, the numerical coefficients are multiplied. These are simply regular numbers in front of the variables. So, we multiply 33 and 55, giving us 1515.
Next, we look at the variables with exponents. We have two types of variables: aa and bb. For each variable, we apply the product of powers rule. For the aa terms: a2×a3=a2+3=a5a^2 \times a^3 = a^{2+3} = a^5. Likewise, for the bb terms: b3×b2=b3+2=b5b^3 \times b^2 = b^{3+2} = b^5.
Combining all the results, we get: 15a5b515a^5b^5
This final expression represents the product of the original two monomials. The key takeaway is that multiplication of monomials involves multiplying coefficients and adding the exponents of like bases. This rule is one of the foundations of algebra and is used repeatedly when simplifying polynomial expressions or solving equations that include variable terms raised to powers.
✅ Correct Answer:
D. 15a⁵b⁵
