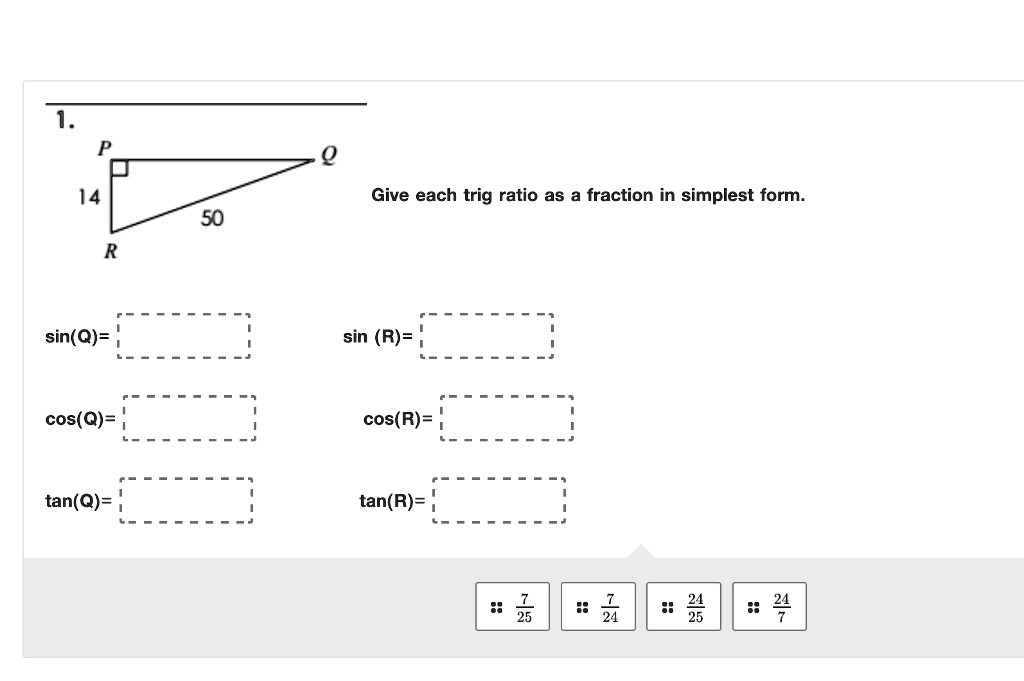
Give each trig ratio as a fraction in simplest form.
The Correct Answer and Explanation is:
To solve this problem, we must first find all the side lengths of triangle △PQR\triangle PQR. The triangle is a right triangle with:
- PQPQ as the hypotenuse = 50
- PRPR = 14
- Angle PP is the right angle
We need to find side QRQR using the Pythagorean Theorem: PQ2=PR2+QR2PQ^2 = PR^2 + QR^2 502=142+QR250^2 = 14^2 + QR^2 2500=196+QR22500 = 196 + QR^2 QR2=2500−196=2304QR^2 = 2500 – 196 = 2304 QR=2304=48QR = \sqrt{2304} = 48
Now the triangle sides are:
- PR=14PR = 14 (opposite angle QQ)
- QR=48QR = 48 (opposite angle RR)
- PQ=50PQ = 50 (hypotenuse)
Trig Ratios:
At angle Q:
- sin(Q) = opposite/hypotenuse = PR / PQ = 1450=725\frac{14}{50} = \frac{7}{25}
- cos(Q) = adjacent/hypotenuse = QR / PQ = 4850=2425\frac{48}{50} = \frac{24}{25}
- tan(Q) = opposite/adjacent = PR / QR = 1448=724\frac{14}{48} = \frac{7}{24}
At angle R:
- sin(R) = opposite/hypotenuse = QR / PQ = 4850=2425\frac{48}{50} = \frac{24}{25}
- cos(R) = adjacent/hypotenuse = PR / PQ = 1450=725\frac{14}{50} = \frac{7}{25}
- tan(R) = opposite/adjacent = QR / PR = 4814=247\frac{48}{14} = \frac{24}{7}
Final Answers:
- sin(Q) = 7/25
- cos(Q) = 24/25
- tan(Q) = 7/24
- sin(R) = 24/25
- cos(R) = 7/25
- tan(R) = 24/7
Explanation
This problem involves applying basic trigonometric ratios—sine, cosine, and tangent—to a right triangle. These ratios are defined as:
- Sine (sin) = opposite side / hypotenuse
- Cosine (cos) = adjacent side / hypotenuse
- Tangent (tan) = opposite side / adjacent side
To use these formulas, we first need all three side lengths of the triangle. Two sides are given: the hypotenuse PQ=50PQ = 50 and one leg PR=14PR = 14. Using the Pythagorean Theorem, we calculate the third side QRQR, the other leg: PQ2=PR2+QR2⇒QR=2500−196=2304=48PQ^2 = PR^2 + QR^2 \Rightarrow QR = \sqrt{2500 – 196} = \sqrt{2304} = 48
Now, each trigonometric function can be calculated at the two acute angles QQ and RR. Remember, the “opposite” and “adjacent” sides depend on which angle you are referring to. For instance, for angle QQ, the side opposite is PRPR, and for angle RR, the opposite is QRQR.
We then simplify each fraction to its lowest terms. This not only answers the question but demonstrates understanding of triangle properties and how to apply trigonometric ratios to solve geometric problems. The values show the consistent relationships between angles and side lengths in right triangles, reinforcing the structure of trigonometry.
