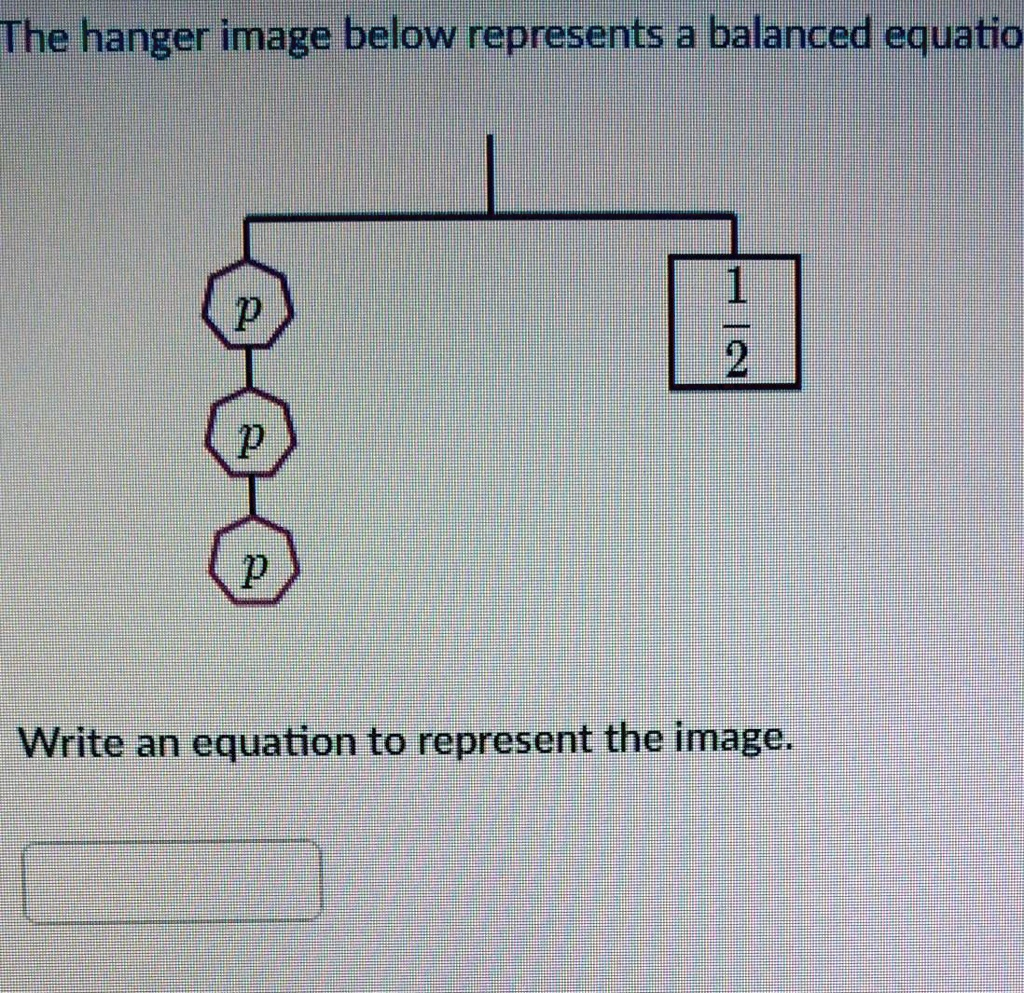
The hanger image below represents a balanced equation p 1 2 p p Write an equation to represent the image.
The Correct Answer and Explanation is:
Correct Answer:
The image represents a balanced hanger with:
- Three weights labeled p on the left side, and
- A single weight labeled 1/2 on the right side.
The balanced hanger implies that the total weight on the left equals the total weight on the right.
The Equation:
p+p+p=12p + p + p = \frac{1}{2}
This simplifies to: 3p=123p = \frac{1}{2}
Explanation
The image shows a hanger balanced in the middle, which is a visual way to represent an equation. In algebra, balance implies equality, meaning both sides of the hanger must have the same total value (or weight).
On the left side of the hanger, there are three identical shapes, each labeled with the variable p. This means each shape has a weight of p, and all together the total weight on the left side is: p+p+p=3pp + p + p = 3p
On the right side of the hanger, there is a single weight represented by a rectangle containing the number 1/2, which means the total weight on the right side is 1/2.
Since the hanger is balanced, the weight on the left side must be equal to the weight on the right side. This leads directly to the equation: 3p=123p = \frac{1}{2}
This equation tells us that three times the value of p is equal to one-half. If you were asked to solve for p, you would divide both sides of the equation by 3: p=12÷3=16p = \frac{1}{2} \div 3 = \frac{1}{6}
Thus, each p has a value of 1/6.
Using visual models like hangers helps students understand the concept of equality and equations in algebra. Instead of just manipulating numbers and symbols, the balance model offers a concrete representation of abstract ideas. It helps build intuition about how changing one side of an equation affects the other side, reinforcing the principle that in an equation, both sides must always remain equal.
