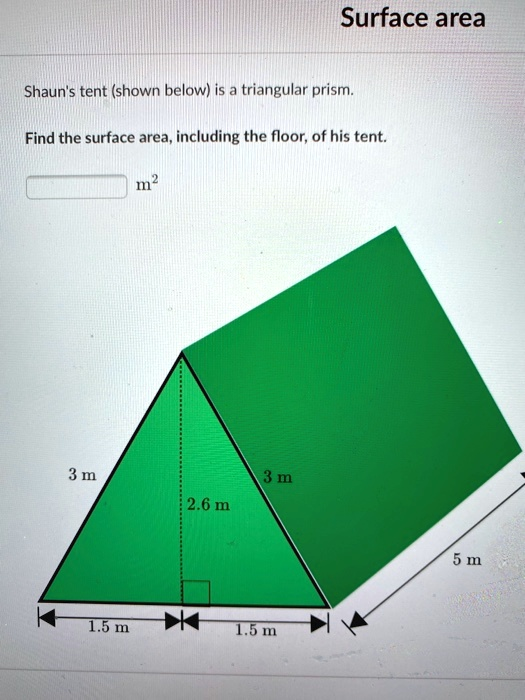
Shaun’s tent (shown below) is a triangular prism. Find the surface area, including the floor, of his tent: Dimensions: Length: 3 m Width: 3 m Height: 2.6 m The formula to calculate the surface area of a triangular prism is: Surface Area = 2 * (base area) + (lateral area) To find the base area, we need to calculate the area of the triangular base. Since it is an equilateral triangle, we can use the formula: Base Area = (sqrt(3) / 4) * (side length)^2 Substituting the values, we get: Base Area = (sqrt(3) / 4) * (3 m)^2 To find the lateral area, we need to calculate the area of the three rectangular faces. The formula for the area of a rectangle is: Area = length * width Substituting the values, we get: Lateral Area = 3 m * 2.6 m + 3 m * 2.6 m + 2.6 m * 2.6 m Finally, we can calculate the surface area by substituting the values into the formula: Surface Area = 2 * (Base Area) + (Lateral Area)
The Correct Answer and Explanation is:
Let’s calculate the surface area of Shaun’s tent, which is a triangular prism. The diagram shows a triangular front face with base 3 meters and height 2.6 meters, and the prism has a length (depth) of 5 meters.
Step 1: Calculate the area of the triangular base
The area of a triangle is: Base Area=12×base×height\text{Base Area} = \frac{1}{2} \times \text{base} \times \text{height}
Given:
- Base = 3 m
- Height = 2.6 m
Base Area=12×3×2.6=3.9 m2\text{Base Area} = \frac{1}{2} \times 3 \times 2.6 = 3.9 \text{ m}^2
Since there are two identical triangular faces: Total Area of Triangular Faces=2×3.9=7.8 m2\text{Total Area of Triangular Faces} = 2 \times 3.9 = 7.8 \text{ m}^2
Step 2: Calculate the lateral (rectangular) surface areas
There are three rectangles forming the sides:
- Bottom rectangle (floor): base × length = 3 m × 5 m = 15 m²
- Two slanted sides (each has side length 3 m and length 5 m):
Each slanted side area=3×5=15 m2\text{Each slanted side area} = 3 \times 5 = 15 \text{ m}^2 Total Lateral Area=15+15+15=45 m2\text{Total Lateral Area} = 15 + 15 + 15 = 45 \text{ m}^2
Step 3: Add base areas and lateral area
Total Surface Area=7.8+45=52.8 m2\text{Total Surface Area} = 7.8 + 45 = \boxed{52.8 \text{ m}^2}
✅ Final Answer: 52.8 m²
✏️ Explanation
To calculate the surface area of Shaun’s tent, we use the formula for the surface area of a triangular prism:
Surface Area = 2 × (Base Area) + Lateral Area.
The tent’s two triangular ends are identical, forming the bases. From the diagram, each triangle has a base of 3 meters and a height of 2.6 meters. Using the triangle area formula 12×base×height\frac{1}{2} \times \text{base} \times \text{height}, each triangular face is 3.93.9 square meters. Since there are two of them, the total area from these faces is 2×3.9=7.82 \times 3.9 = 7.8 m².
The lateral area comes from the three rectangular sides of the prism:
- The bottom rectangle (the floor of the tent) has dimensions 3 m by 5 m, so its area is 15 m².
- Each slanted side is a rectangle with dimensions 3 m by 5 m, resulting in 15 m² each.
Adding these: 15+15+15=4515 + 15 + 15 = 45 m².
Finally, we sum the triangle faces (7.8 m²) and the rectangular sides (45 m²) to get the total surface area: 52.8 m2\boxed{52.8 \text{ m}^2}
This includes all outer sides and the floor, as required.
