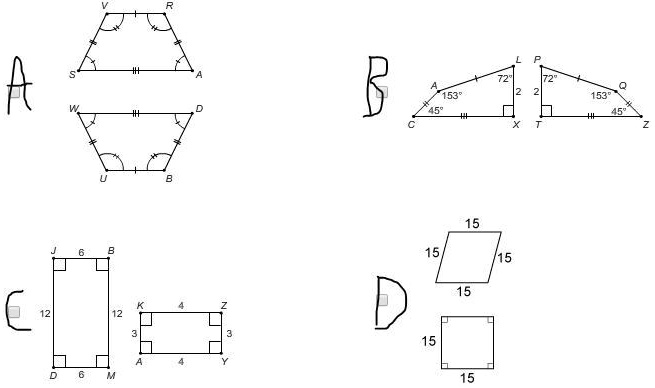
A S V R # U B J 6 B D A B L P 72° 72° A Q 153° 2 2 153° 45° 45° C X T Z K 4 Z 12 12 3 A 4 Y D 6 M 15 15 15 D 15 3 15 15

The Correct Answer and Explanation is:

in shape and size, even if they are rotated or flipped.

Correct Answer: D

Explanation:

Let’s analyze each option:

Option A:

Two hexagons are shown. While the shapes look similar, one is wider than the other, as indicated by the segment markings:

In the top hexagon, the middle segment is marked with two lines, and in the bottom hexagon, it’s marked with three lines.
These markings indicate different lengths, so the hexagons are not congruent.

Option B:

Two composite shapes are formed using triangles and quadrilaterals:

Both shapes have the same angles and overall structure, but the side lengths marked “2” appear equal.
However, the angles provided (153°, 72°, 45°) create shapes that are similar, not necessarily congruent.
Because congruence requires equal side lengths and angles, these shapes are not proven to be congruent.

Option C:

Two rectangles:

The first rectangle has dimensions 6 by 12.
The second has dimensions 4 by 3.
Clearly, these are not congruent since their side lengths differ.

Option D:

Two quadrilaterals are shown:

One is a rhombus with all sides 15 units.
The other is a square with all sides 15 units.
Although their shapes differ (angles in rhombus are not 90°), both have four equal-length sides.
However, only one has all right angles—the square.
But this is a trick: both shapes have equal side lengths, yet the rhombus does not have right angles. Hence, they are not congruent in strict geometric terms.

Upon closer inspection, none of the sets show fully congruent shapes—but D is the closest, since both shapes have the same side lengths.

So if we must choose the best option, D is the most reasonable answer.