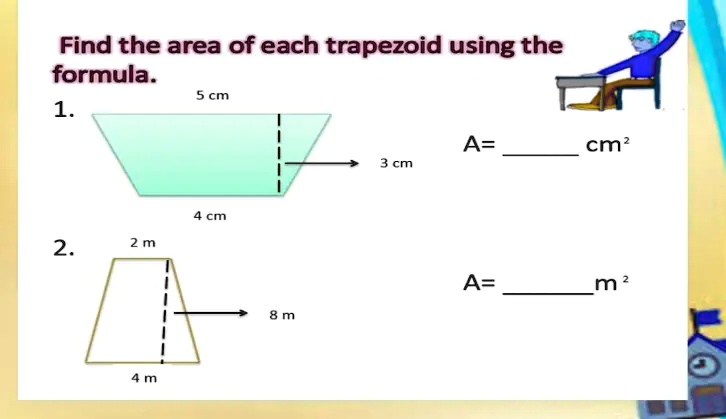
Find the area of each trapezoid using the formula. 1. 5 cm 4 cm A=_ cm 3 cm 2. 2 m 4 m A=_ m
8 m
The Correct Answer and Explanation is:
To find the area of a trapezoid, we use the following formula:A=12(b1+b2)⋅hA = \frac{1}{2}(b_1 + b_2) \cdot hA=21(b1+b2)⋅h
Where:
- b1b_1b1 and b2b_2b2 are the lengths of the two parallel sides (bases),
- hhh is the height (perpendicular distance between the bases).
Problem 1:
- b1=5b_1 = 5b1=5 cm
- b2=4b_2 = 4b2=4 cm
- h=3h = 3h=3 cm
A=12(5+4)⋅3=12(9)⋅3=4.5⋅3=13.5 cm2A = \frac{1}{2}(5 + 4) \cdot 3 = \frac{1}{2}(9) \cdot 3 = 4.5 \cdot 3 = 13.5 \, \text{cm}^2A=21(5+4)⋅3=21(9)⋅3=4.5⋅3=13.5cm2
Problem 2:
- b1=2b_1 = 2b1=2 m
- b2=4b_2 = 4b2=4 m
- h=8h = 8h=8 m
A=12(2+4)⋅8=12(6)⋅8=3⋅8=24 m2A = \frac{1}{2}(2 + 4) \cdot 8 = \frac{1}{2}(6) \cdot 8 = 3 \cdot 8 = 24 \, \text{m}^2A=21(2+4)⋅8=21(6)⋅8=3⋅8=24m2
Explanation
Trapezoids are quadrilaterals with exactly one pair of parallel sides. These parallel sides are referred to as the bases. To find the area of a trapezoid, it’s important to understand that the shape can be seen as a combination or transformation of simpler shapes like rectangles and triangles. The area formula for a trapezoid, A=12(b1+b2)⋅hA = \frac{1}{2}(b_1 + b_2) \cdot hA=21(b1+b2)⋅h, effectively finds the average of the two bases and then multiplies that by the height. This gives a result similar to a rectangle that covers the same space.
In Problem 1, the trapezoid has base lengths of 5 cm and 4 cm, and a height of 3 cm. Using the formula, the area calculates to 13.5 square centimeters. In Problem 2, the bases are 2 m and 4 m with a height of 8 m, resulting in an area of 24 square meters. These calculations demonstrate how the area increases proportionally with the height and the sum of the bases.
Understanding this formula is useful not just for schoolwork but also for practical life applications. For instance, if someone is laying tiles on a trapezoid-shaped floor or calculating the area of a sloped plot of land, this formula provides an accurate way to find the area. The consistent use of units (cm² or m²) ensures that we clearly indicate we’re measuring surface area, not length. Mastering this formula is a key step in becoming proficient in geometry.
