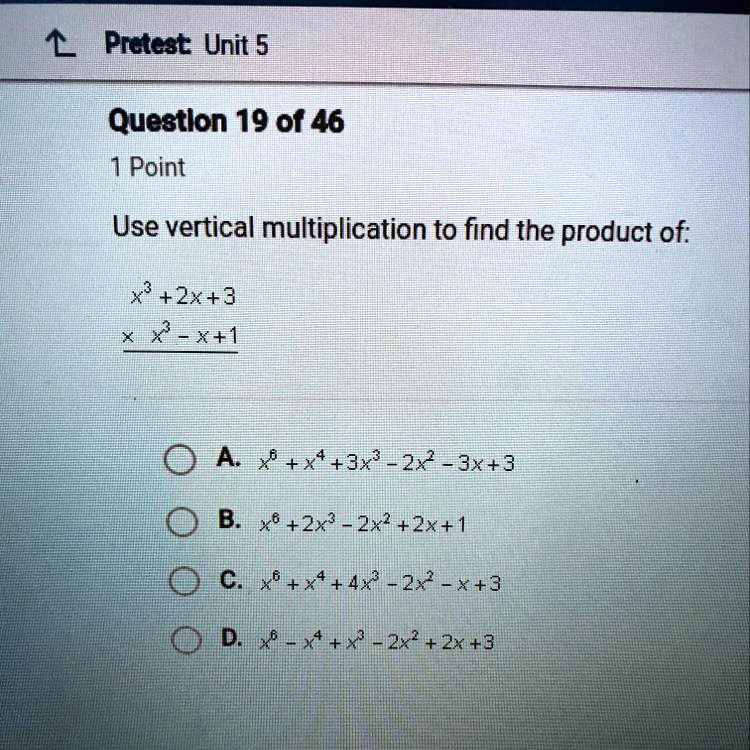
Pretest: Unit 5 Question 19 of 46 1 Point Use vertical multiplication to find the product of:
A.
B.
C.
The Correct Answer and Explanation is:
To find the product of(x3+2x+3)(x2−x+1),(x^3 + 2x + 3)(x^2 – x + 1),(x3+2x+3)(x2−x+1),
we’ll use vertical multiplication (also called the distributive or box method).
Step-by-step Multiplication:
Multiply each term of the second polynomial by each term of the first polynomial:
- Multiply x3+2x+3x^3 + 2x + 3×3+2x+3 by x2x^2×2:
x2(x3+2x+3)=x5+2×3+3x2x^2(x^3 + 2x + 3) = x^5 + 2x^3 + 3x^2×2(x3+2x+3)=x5+2×3+3×2
- Multiply x3+2x+3x^3 + 2x + 3×3+2x+3 by −x-x−x:
−x(x3+2x+3)=−x4−2×2−3x-x(x^3 + 2x + 3) = -x^4 – 2x^2 – 3x−x(x3+2x+3)=−x4−2×2−3x
- Multiply x3+2x+3x^3 + 2x + 3×3+2x+3 by 111:
1(x3+2x+3)=x3+2x+31(x^3 + 2x + 3) = x^3 + 2x + 31(x3+2x+3)=x3+2x+3
Now, add the results together:
- x5x^5×5
- −x4-x^4−x4
- 2×3+x3=3x32x^3 + x^3 = 3x^32×3+x3=3×3
- 3×2−2×2=x23x^2 – 2x^2 = x^23×2−2×2=x2
- −3x+2x=−x-3x + 2x = -x−3x+2x=−x
- +3+3+3
Final Answer:
x5−x4+3×3+x2−x+3x^5 – x^4 + 3x^3 + x^2 – x + 3×5−x4+3×3+x2−x+3
This matches Option C.
Explanation
To solve this polynomial multiplication problem, we use vertical (or distributive) multiplication. This technique ensures every term from one polynomial is multiplied by every term from the other, just like in traditional multiplication with numbers.
Given the polynomials x3+2x+3x^3 + 2x + 3×3+2x+3 and x2−x+1x^2 – x + 1×2−x+1, we distribute each term in the second polynomial across the first. We begin by multiplying the first polynomial by the highest-degree term in the second polynomial, which is x2x^2×2. This gives us terms of degree 5, 3, and 2.
Next, we multiply the entire first polynomial by −x-x−x, carefully applying the negative sign to each resulting term. Then, we do the same for the constant 1.
Once we have all the partial products, we combine like terms — that is, terms with the same degree (same exponent on xxx). This step requires attention to detail to ensure no signs are missed and all like terms are correctly added or subtracted.
After simplifying, we get the resulting polynomial:x5−x4+3×3+x2−x+3.x^5 – x^4 + 3x^3 + x^2 – x + 3.×5−x4+3×3+x2−x+3.
Matching this with the answer choices, we find that it corresponds to Option C. This method helps break down a potentially complex problem into manageable parts, making it easier to track each multiplication and avoid mistakes.
✅ Correct Answer: C.
