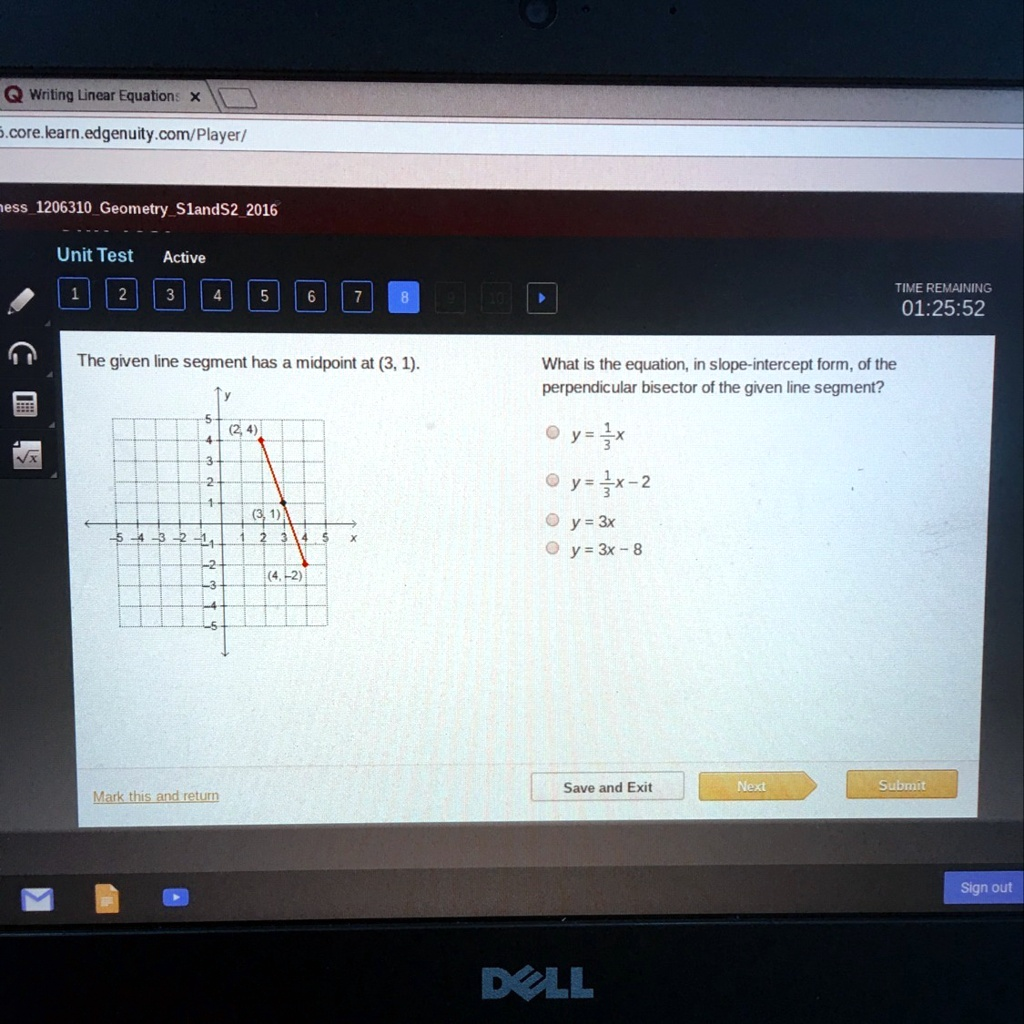
The given line segment has a midpoint at (3,1). What is the equation, in slope-intercept form, of the perpendicular bisector of the given line segment? Writing Linear Equation: corelearn.edgenuity.com/Player/ ess 1206310 Geometry SlandS2 2016 Unit Test Active TIME REMAINING 01:25:52 The given line segment has a midpoint at (3,1). What is the equation, in slope-intercept form, of the perpendicular bisector of the given line segment? Y = y = ix-2 y = 3x y = 3x – 8 Save and Exit Next Submit Mark this and return Sign out DeLL
The Correct Answer and Explanation is:
To find the equation of the perpendicular bisector of the given line segment, we need to follow these steps:
Step 1: Identify the endpoints of the line segment
From the image, the endpoints are:
- A=(2,4)A = (2, 4)A=(2,4)
- B=(4,−2)B = (4, -2)B=(4,−2)
Step 2: Find the midpoint
The midpoint formula is:Midpoint=(x1+x22,y1+y22)=(2+42,4+(−2)2)=(3,1)\text{Midpoint} = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) = \left( \frac{2 + 4}{2}, \frac{4 + (-2)}{2} \right) = (3, 1)Midpoint=(2×1+x2,2y1+y2)=(22+4,24+(−2))=(3,1)
✅ This matches the given midpoint.
Step 3: Find the slope of the line segment AB
Slope formula:m=y2−y1x2−x1=−2−44−2=−62=−3m = \frac{y_2 – y_1}{x_2 – x_1} = \frac{-2 – 4}{4 – 2} = \frac{-6}{2} = -3m=x2−x1y2−y1=4−2−2−4=2−6=−3
Step 4: Find the slope of the perpendicular bisector
The perpendicular slope is the negative reciprocal of −3-3−3, which is:13\frac{1}{3}31
Step 5: Use point-slope form to write the equation
We know the perpendicular bisector passes through the midpoint (3,1)(3, 1)(3,1) and has slope 13\frac{1}{3}31.
Point-slope form:y−y1=m(x−x1)y – y_1 = m(x – x_1)y−y1=m(x−x1)
Substitute:y−1=13(x−3)y – 1 = \frac{1}{3}(x – 3)y−1=31(x−3)
Step 6: Convert to slope-intercept form (y = mx + b)
y−1=13x−1y=13x−1+1y=13xy – 1 = \frac{1}{3}x – 1 \\ y = \frac{1}{3}x – 1 + 1 \\ y = \frac{1}{3}xy−1=31x−1y=31x−1+1y=31x
✅ Final Answer:
y=13x\boxed{y = \frac{1}{3}x}y=31x
Correct Option:
- ✅ A. y=13xy = \frac{1}{3}xy=31x
Explanation
To determine the equation of the perpendicular bisector of a line segment, we need to understand two geometric concepts: the midpoint and perpendicular slope. The perpendicular bisector is a line that cuts a segment exactly in half at a 90° angle. First, we identify the endpoints of the segment from the graph: (2, 4) and (4, -2). Using the midpoint formula, we calculate the midpoint as (3,1)(3, 1)(3,1), which matches the one given.
Next, we calculate the slope of the original line segment using the slope formula: rise over run. The slope from (2, 4) to (4, -2) is −62=−3\frac{-6}{2} = -32−6=−3. A line perpendicular to this must have a slope that is the negative reciprocal of -3, which is 13\frac{1}{3}31. This means the perpendicular bisector has a slope of 13\frac{1}{3}31.
Now that we have the slope and a point the line goes through (3,1)(3, 1)(3,1), we can use the point-slope form of a line: y−y1=m(x−x1)y – y_1 = m(x – x_1)y−y1=m(x−x1). Plugging in our values gives us:y−1=13(x−3)y – 1 = \frac{1}{3}(x – 3)y−1=31(x−3)
Distributing and simplifying converts this to slope-intercept form: y=13xy = \frac{1}{3}xy=31x.
This equation describes a line with slope 13\frac{1}{3}31 that passes through the midpoint and is perpendicular to the original segment. Thus, the correct answer is y=13xy = \frac{1}{3}xy=31x.
