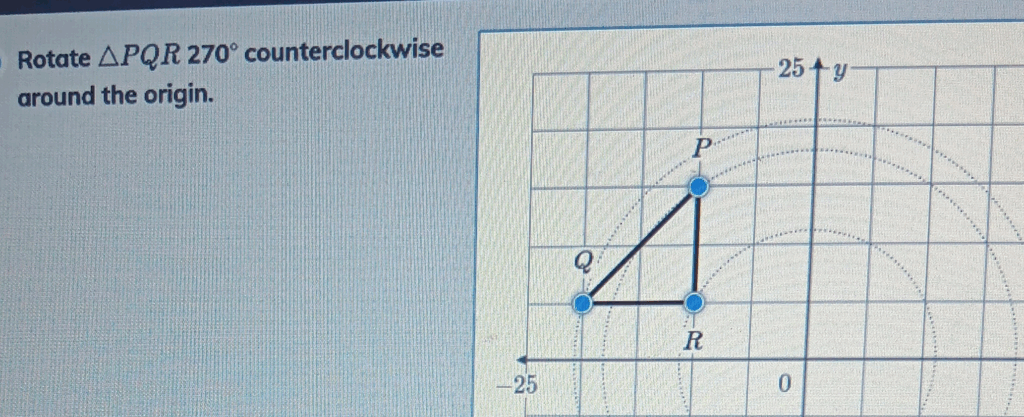
Rotate PQR 270
counterclockwise around the origin.
The Correct Answer and Explanation is:
The vertices of the rotated triangle, ΔP’Q’R’, are:
- P’ (20, 10)
- Q’ (10, 20)
- R’ (10, 10)
Explanation
The objective is to rotate triangle PQR by 270 degrees counterclockwise around the origin (0, 0). A rotation is a rigid transformation, which means the size and shape of the triangle will be preserved; only its orientation and position will change. The process involves three main steps: identifying the original coordinates, applying the rotation rule, and determining the new coordinates.
Step 1: Determine the coordinates of the original vertices.
First, we must identify the coordinates of the vertices P, Q, and R from the graph. By observing the axes, we can see that each grid line represents 5 units.
- Vertex P is located 2 grid lines to the left of the y-axis and 4 grid lines above the x-axis. Therefore, its coordinates are P = (-10, 20).
- Vertex Q is located 4 grid lines to the left of the y-axis and 2 grid lines above the x-axis. Its coordinates are Q = (-20, 10).
- Vertex R is located 2 grid lines to the left of the y-axis and 2 grid lines above the x-axis. Its coordinates are R = (-10, 10).
Step 2: Understand the rule for a 270° counterclockwise rotation.
A 270° counterclockwise rotation around the origin follows a specific algebraic rule. For any point with coordinates (x, y), a 270° counterclockwise rotation transforms it to a new point with coordinates (y, -x). This means the original x and y values swap positions, and the new y-coordinate becomes the opposite of the original x-coordinate. This transformation is also equivalent to a 90° clockwise rotation.
Step 3: Apply the rotation rule to each vertex.
We now apply the rule (x, y) → (y, -x) to each vertex of ΔPQR to find the coordinates of the rotated triangle, ΔP’Q’R’.
- For P(-10, 20):
The new coordinates P’ will be (20, -(-10)), which simplifies to P'(20, 10). - For Q(-20, 10):
The new coordinates Q’ will be (10, -(-20)), which simplifies to Q'(10, 20). - For R(-10, 10):
The new coordinates R’ will be (10, -(-10)), which simplifies to R'(10, 10).
By completing these steps, we have successfully rotated ΔPQR 270° counterclockwise around the origin to its new position, ΔP’Q’R’, with vertices at P'(20, 10), Q'(10, 20), and R'(10, 10).
