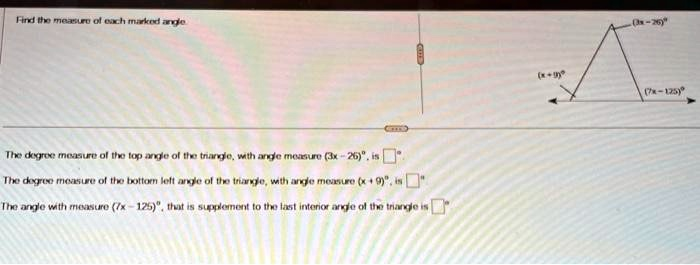
1. The degree measure of the top angle of the triangle, with angle measure (3x-26) is . 2. The degree measure of the bottom left angle of the triangle, with angle measure (x+9) is . 3. The angle with measure (7x-125) that is supplementary to the last interior angle of the triangle is __
The Correct Answer and Explanation is:
The degree measure of the top angle of the triangle, with angle measure (3x-26)°, is 82°.
2. The degree measure of the bottom left angle of the triangle, with angle measure (x+9)°, is 45°.
3. The angle with measure (7x-125)°, that is supplementary to the last interior angle of the triangle is 127°.
Explanation:
To determine the measure of each angle, we must first find the value of x. The solution relies on the Exterior Angle Theorem, a fundamental concept in geometry. This theorem states that the measure of an exterior angle of a triangle is equal to the sum of the measures of its two non-adjacent (or remote) interior angles.
Step 1: Set up the equation
Based on the provided image, we can identify the following angles:
- The two remote interior angles are the top angle, (3x – 26)°, and the bottom-left angle, (x + 9)°.
- The exterior angle at the bottom-right vertex is (7x – 125)°.
Applying the Exterior Angle Theorem, we set the sum of the two remote interior angles equal to the exterior angle:
(3x – 26) + (x + 9) = 7x – 125
Step 2: Solve the equation for x
First, combine the like terms on the left side of the equation:
4x – 17 = 7x – 125
Next, isolate the variable x. We can do this by subtracting 4x from both sides:
-17 = 3x – 125
Then, add 125 to both sides to isolate the term with x:
108 = 3x
Finally, divide by 3 to find the value of x:
x = 36
Step 3: Calculate the measure of each angle
Now that we have the value of x, we can substitute it back into the expressions for each angle:
- Top Angle:
(3x – 26)° = 3(36) – 26 = 108 – 26 = 82° - Bottom Left Angle:
(x + 9)° = 36 + 9 = 45° - Exterior Angle (supplementary to the bottom right interior angle):
(7x – 125)° = 7(36) – 125 = 252 – 125 = 127°
As a final check, the third interior angle is 180° – 127° = 53°. The sum of the three interior angles is 82° + 45° + 53° = 180°, which confirms the calculations are correct.
