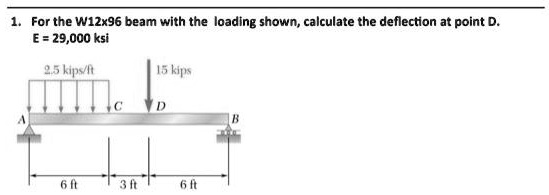
For the W12x96 beam with the loading shown, calculate the deflection at point D. E = 29,000 ksi 2.5 kips/ft A 15 kips D B 6 ft 3 ft 6 ft
The Correct Answer and Explanation is:
Here is the step-by-step solution to calculate the deflection at point D.
Final Answer:
The deflection at point D is 0.0860 inches downwards.
Explanation
This problem is solved by applying the principle of superposition. This principle allows a complex loading scenario to be broken down into simpler, standard cases. The total deflection at any point is the algebraic sum of the deflections caused by each load acting independently on the beam.
Step 1: Determine Beam Properties and Convert Units
First, the necessary properties for the W12x96 steel beam are obtained from a standard steel section table. The modulus of elasticity (E) is given. To ensure consistent units for the calculation, all measurements are converted to kips and inches.
- Modulus of Elasticity (E) = 29,000 ksi (kips per square inch)
- Moment of Inertia for a W12x96 beam (Iₓ) = 833 in⁴
- Flexural Rigidity (EI) = 29,000 ksi × 833 in⁴ = 24,157,000 kip·in²
- Total Beam Length (L) = 6 ft + 3 ft + 6 ft = 15 ft = 180 in
- Distributed Load (w) = 2.5 kips/ft = 2.5 / 12 kips/in ≈ 0.20833 kips/in
- Concentrated Load (P) = 15 kips
Step 2: Apply the Principle of Superposition
The problem is divided into two separate cases:
- Case 1: A simply supported beam with only the partial distributed load of 2.5 kips/ft over the first 6 ft (72 inches).
- Case 2: A simply supported beam with only the concentrated load of 15 kips at point D, located 9 ft (108 inches) from support A.
The total deflection at D (δ_D) will be the sum of the deflections from each case (δ_D1 + δ_D2).
Step 3: Calculate Deflection for Case 1 (Distributed Load)
The formula for deflection at a point x in the unloaded segment of a beam with a partial uniform load w from support A to a distance a is:
δ(x) = [w⋅a²⋅(L-x) / (24⋅E⋅I⋅L)] ⋅ [2⋅L⋅x – x² – a²]
Here, w = 0.20833 kips/in, a = 72 in, L = 180 in, and we are finding deflection at x = 108 in.
δ_D1 = [0.20833⋅(72)²⋅(180-108) / (24⋅24,157,000⋅180)] ⋅ [2⋅180⋅108 – (108)² – (72)²]
δ_D1 = [77,759.6 / (1.0435 × 10¹¹)] ⋅ [38,880 – 11,664 – 5,184]
δ_D1 = (7.452 × 10⁻⁷) ⋅ (22,032) = 0.0164 in
Step 4: Calculate Deflection for Case 2 (Concentrated Load)
The formula for deflection under a concentrated load P located at a distance a from one support and b from the other is:
δ = (P⋅a²⋅b²) / (3⋅E⋅I⋅L)
Here, P = 15 kips, a = 108 in, and b = 180 – 108 = 72 in.
δ_D2 = [15 ⋅ (108)² ⋅ (72)²] / [3 ⋅ 24,157,000 ⋅ 180]
δ_D2 = [906,992,640] / [13,044,780,000] = 0.0695 in
Step 5: Calculate Total Deflection
The total deflection at point D is the sum of the deflections from both cases.
δ_D = δ_D1 + δ_D2
δ_D = 0.0164 in + 0.0695 in = 0.0859 in
Rounding to three significant figures, the final deflection at point D is 0.0860 inches downwards.
