Given the parametric equations:

𝑥

1
−
𝑡
2
,

𝑦

1
+
𝑡
x=1−t
2
,y=1+t
We are to find:

𝑑
𝑦
𝑑
𝑥
dx
dy
​
— the first derivative of
𝑦
y with respect to
𝑥
x,

𝑑
2
𝑦
𝑑
𝑥
2
dx
2

d
2
y
​
— the second derivative of
𝑦
y with respect to
𝑥
x,

without eliminating the parameter.

Step 1: First Derivative
𝑑
𝑦
𝑑
𝑥
dx
dy
​

Using parametric differentiation, the first derivative is given by:

𝑑
𝑦
𝑑

𝑥

𝑑
𝑦
𝑑
𝑡
𝑑
𝑥
𝑑
𝑡
dx
dy
​
=
dt
dx
​

dt
dy
​

​

Differentiate
𝑥
x and
𝑦
y with respect to
𝑡
t:

𝑑
𝑥
𝑑

𝑡

𝑑
𝑑
𝑡
(
1
−
𝑡
2

)

−
2
𝑡
dt
dx
​
=
dt
d
​
(1−t
2
)=−2t

𝑑
𝑦
𝑑

𝑡

𝑑
𝑑
𝑡
(
1
+
𝑡

)

1
dt
dy
​
=
dt
d
​
(1+t)=1

So,

𝑑
𝑦
𝑑

𝑥

1
−
2

𝑡

−
1
2
𝑡
dx
dy
​
=
−2t
1
​
=−
2t
1
​

Step 2: Second Derivative
𝑑
2
𝑦
𝑑
𝑥
2
dx
2

d
2
y
​

The second derivative in parametric form is given by:

𝑑
2
𝑦
𝑑
𝑥

2

𝑑
𝑑
𝑡
(
𝑑
𝑦
𝑑
𝑥
)
÷
𝑑
𝑥
𝑑
𝑡
dx
2

d
2
y
​
=
dt
d
​
(
dx
dy
​
)÷
dt
dx
​

We already have
𝑑
𝑦
𝑑

𝑥

−
1
2
𝑡
dx
dy
​
=−
2t
1
​
, so compute its derivative with respect to
𝑡
t:

𝑑
𝑑
𝑡
(
−
1
2
𝑡

)

1
2
𝑡
2
dt
d
​
(−
2t
1
​
)=
2t
2

1
​

Now divide by
𝑑
𝑥
𝑑

𝑡

−
2
𝑡
dt
dx
​
=−2t:

𝑑
2
𝑦
𝑑
𝑥

2

1
2
𝑡
2
−
2

𝑡

−
1
4
𝑡
3
dx
2

d
2
y
​
=
−2t
2t
2

1
​

​
=−
4t
3

1
​

Final Answers:
𝑑
𝑦
𝑑

𝑥

−
1
2
𝑡
,
𝑑
2
𝑦
𝑑
𝑥

2

−
1
4
𝑡
3
dx
dy
​
=−
2t
1
​
,
dx
2

d
2
y
​
=−
4t
3

1
​

Explanation (300 words):
When working with parametric equations, such as

𝑥

1
−
𝑡
2
x=1−t
2
and

𝑦

1
+
𝑡
y=1+t, we treat both
𝑥
x and
𝑦
y as functions of a third variable
𝑡
t, known as the parameter. Instead of expressing
𝑦
y directly in terms of
𝑥
x, we differentiate each with respect to
𝑡
t, and use these derivatives to find the derivatives of
𝑦
y with respect to
𝑥
x.

To find the first derivative
𝑑
𝑦
𝑑
𝑥
dx
dy
​
, we apply the chain rule of calculus. Since
𝑑
𝑦
/
𝑑

𝑥

(
𝑑
𝑦
/
𝑑
𝑡
)
/
(
𝑑
𝑥
/
𝑑
𝑡
)
dy/dx=(dy/dt)/(dx/dt), we compute the derivatives:

𝑑
𝑦
/
𝑑

𝑡

1
dy/dt=1, since

𝑦

1
+
𝑡
y=1+t,

𝑑
𝑥
/
𝑑

𝑡

−
2
𝑡
dx/dt=−2t, because

𝑥

1
−
𝑡
2
x=1−t
2
.

Substituting, we get
𝑑
𝑦
𝑑

𝑥

1
−
2

𝑡

−
1
2
𝑡
dx
dy
​
=
−2t
1
​
=−
2t
1
​
.

To find the second derivative
𝑑
2
𝑦
𝑑
𝑥
2
dx
2

d
2
y
​
, we use the formula:

𝑑
2
𝑦
𝑑
𝑥

2

𝑑
𝑑
𝑡
(
𝑑
𝑦
𝑑
𝑥
)
÷
𝑑
𝑥
𝑑
𝑡
dx
2

d
2
y
​
=
dt
d
​
(
dx
dy
​
)÷
dt
dx
​

This involves differentiating
−
1
2
𝑡
−
2t
1
​
with respect to
𝑡
t, which gives
1
2
𝑡
2
2t
2

1
​
, and then dividing this result by
−
2
𝑡
−2t, the derivative of
𝑥
x. Thus:

𝑑
2
𝑦
𝑑
𝑥

2

1
2
𝑡
2
−
2

𝑡

−
1
4
𝑡
3
dx
2

d
2
y
​
=
−2t
2t
2

1
​

​
=−
4t
3

1
​

This process allows us to compute the derivatives directly from the parametric equations without needing to eliminate the parameter.

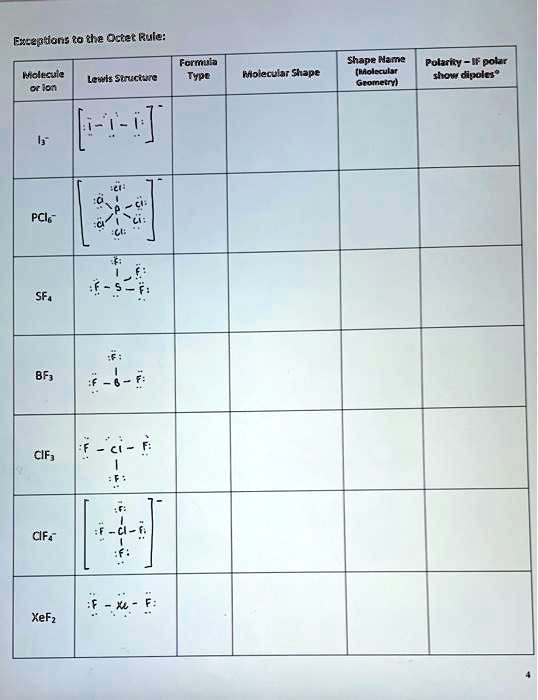
The Correct Answer and Explanation is:

Completed Chemistry Worksheet: Exceptions to the Octet Rule

Molecule or Ion	Lewis Structure	Formula Type	Molecular Shape (Description)	Shape Name (Molecular Geometry)	Polarity – if polar show dipoles
I₃⁻	[ :Ï — Ï — Ï: ]⁻ (Central I has 3 lone pairs)	AX₂E₃	The central Iodine atom is bonded to two other Iodine atoms in a straight line, with three lone pairs arranged in a plane around the central atom’s equator.	Linear	Nonpolar (The symmetrical arrangement of atoms causes the dipoles to cancel.)
PCl₆⁻	[P bonded to 6 Cl]⁻ (P has no lone pairs)	AX₆	A central Phosphorus atom is bonded to six Chlorine atoms, with four in a square plane and one above and one below the plane.	Octahedral	Nonpolar (The symmetrical octahedral geometry causes all bond dipoles to cancel out.)
SF₄	S bonded to 4 F (S has one lone pair)	AX₄E₁	A central Sulfur atom is bonded to four Fluorine atoms. The lone pair on the sulfur atom pushes the bonds away, creating a shape that resembles a seesaw.	Seesaw	Polar (The shape is asymmetrical due to the lone pair. There is a net dipole moment pointing towards the fluorine atoms.)
BF₃	B bonded to 3 F (B has an incomplete octet)	AX₃	A central Boron atom is bonded to three Fluorine atoms, all lying in the same plane and spaced 120° apart.	Trigonal Planar	Nonpolar (The symmetrical arrangement of the B-F bonds in a plane causes the dipoles to cancel.)
ClF₃	Cl bonded to 3 F (Cl has two lone pairs)	AX₃E₂	A central Chlorine atom is bonded to three Fluorine atoms. Two lone pairs on the chlorine push the bonds into a T-shape.	T-shaped	Polar (The shape is asymmetrical. The bond dipoles do not cancel, resulting in a net dipole moment along the stem of the ‘T’.)
ClF₄⁻	[Cl bonded to 4 F]⁻ (Cl has two lone pairs)	AX₄E₂	A central Chlorine atom is bonded to four Fluorine atoms that lie in a single plane. Two lone pairs are located above and below this plane.	Square Planar	Nonpolar (Although the bonds are polar, the symmetrical arrangement of the four Fluorine atoms around the central Chlorine causes their dipoles to cancel out.)
XeF₂	Xe bonded to 2 F (Xe has three lone pairs)	AX₂E₃	A central Xenon atom is bonded to two Fluorine atoms. Three lone pairs on the Xenon atom are arranged in a plane, forcing the Fluorine atoms to opposite sides.	Linear	Nonpolar (The two Xe-F bonds are on opposite sides of the central atom, so their dipoles are equal and opposite, and they cancel out.)

thumb_upthumb_down