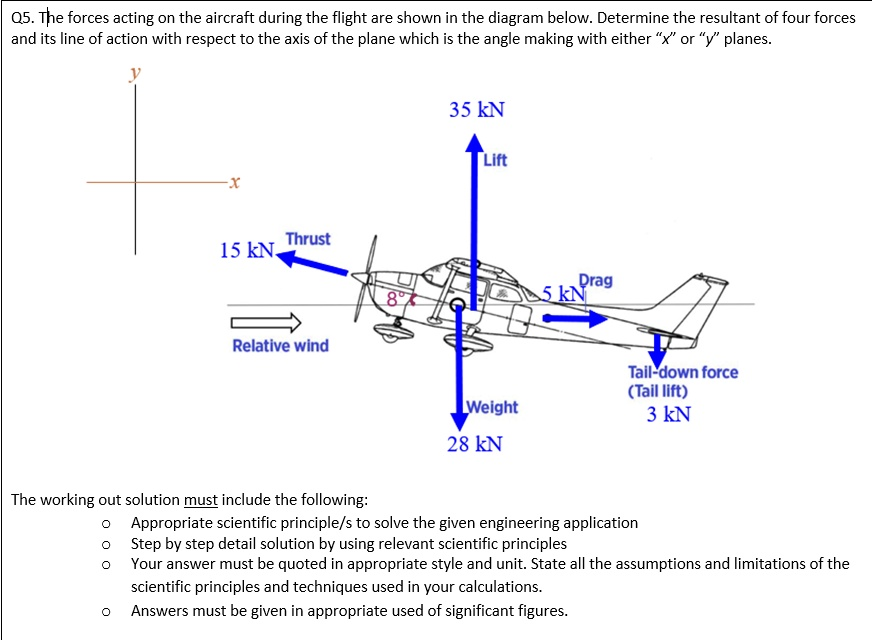
The forces acting on the aircraft during the flight are shown in the diagram below. Determine the resultant of four forces and its line of action with respect to the axis of the plane which is the angle making with either \”x\” or \”y\” planes. y x Thrust 15 kN 35 kN Lift 8
Drag 5 kN Relative wind Weight 28 kN Tail-down force (Tail lift) 3 kN The working out solution must include the following: \circ Appropriate scientific principle/s to solve the given engineering application \circ Step by step detail solution by using relevant scientific principles \circ Your answer must be quoted in appropriate style and unit. State all the assumptions and limitations of the scientific principles and techniques used in your calculations. \circ Answers must be given in appropriate used of significant figures.
The Correct Answer and Explanation is:
Solution: Resultant Force on an Aircraft
1. Appropriate Scientific Principle/s
This problem is solved using the principles of vector addition from engineering mechanics. The resultant of a system of forces is the single force that has the same effect as all the individual forces combined. The method employed is the resolution of forces into components. Each force vector is broken down into its orthogonal components along a Cartesian coordinate system (x and y axes). These components are then algebraically summed to find the components of the resultant force. Finally, the magnitude and direction of the resultant vector are calculated using the Pythagorean theorem and trigonometry.
2. Step-by-Step Detailed Solution
The solution involves determining the net force in the horizontal (x) and vertical (y) directions and then combining them to find the final resultant force and its direction.
Step 1: Resolve all forces into x and y components.
We establish a coordinate system where the x-axis is horizontal (positive to the right) and the y-axis is vertical (positive upwards). All five forces shown are resolved accordingly.
- Lift (F_L): Acts purely in the +y direction.
- F_Lx = 0 kN
- F_Ly = +35 kN
- Weight (F_W): Acts purely in the -y direction.
- F_Wx = 0 kN
- F_Wy = -28 kN
- Drag (F_D): Acts purely in the -x direction.
- F_Dx = -5 kN
- F_Dy = 0 kN
- Tail-down force (F_TDF): Acts purely in the -y direction.
- F_TDFx = 0 kN
- F_TDFy = -3 kN
- Thrust (F_T): Acts at 8° above the negative x-axis.
- F_Tx = -15 * cos(8°) = -14.85 kN
- F_Ty = +15 * sin(8°) = +2.09 kN
Step 2: Sum the components to find the resultant components (Rx, Ry).
- Sum of x-components (Rx):
Rx = F_Lx + F_Wx + F_Dx + F_TDFx + F_Tx
Rx = 0 + 0 – 5 + 0 – 14.85 = -19.85 kN - Sum of y-components (Ry):
Ry = F_Ly + F_Wy + F_Dy + F_TDFy + F_Ty
Ry = 35 – 28 + 0 – 3 + 2.09 = +6.09 kN
Step 3: Calculate the magnitude of the resultant force (R).
Using the Pythagorean theorem, R = √(Rx² + Ry²).
R = √((-19.85)² + (6.09)²) = √(394.02 + 37.09) = √431.11
R = 20.76 kN
Step 4: Calculate the direction (line of action) of the resultant force (θ).
Since Rx is negative and Ry is positive, the resultant force lies in the second quadrant. We find the angle θ with respect to the negative x-axis.
θ = tan⁻¹(|Ry / Rx|)
θ = tan⁻¹(6.09 / 19.85) = tan⁻¹(0.3068)
θ = 17.06°
Rounding to an appropriate number of significant figures, we get:
- Resultant Force (R): 20.8 kN
- Direction (θ): 17.1° above the negative horizontal axis.
3. Assumptions and Limitations
- Assumptions:
- The problem is analyzed as a two-dimensional system, with all forces acting within the x-y plane.
- For calculating the resultant force, all forces are treated as concurrent (acting through a single point). This allows for vector addition without considering moments.
- Although the question mentions “four forces,” this solution assumes it is a general reference to the primary flight forces, and that a complete analysis requires including all five force vectors shown in the diagram.
- Limitations:
- This is a simplified model. The actual forces on an aircraft are distributed loads, not single point forces.
- The calculation determines the net force but does not provide information about the resultant moment or torque on the aircraft. Therefore, it cannot be used to determine the aircraft’s rotational acceleration or stability. The “line of action” is found as an angle only, not its specific location relative to the aircraft’s center of gravity.
4. Final Answer
The resultant of the forces acting on the aircraft has a magnitude of 20.8 kN and its line of action is at an angle of 17.1° measured counter-clockwise (upwards) from the negative x-axis.thumb_upthumb_down
